Getting Started with MATHEMATICA
|
 |
This short primer consists primarily of a sequence of examples which are intended to illustrate
basic features of the mathematical software package MATHEMATICA, which is installed in the
Computer Labs on the University of Oklahoma campus.
For optimal use, it is suggested that you initiate a MATHEMATICA session and attempt to carry out the
examples that are discussed.
- Starting and Stopping.
- To start:
Sit down at a PC or MAC in any of the A&S Computer Labs and choose
MATHEMATICA from the Windows Start menu or icon
grouping.
- To stop:
select Exit from the
File menu in the upper left corner of the MATHEMATICA window.
- Getting help:
There is a very extensive and well-organized Help facility built into
MATHEMATICA. This may be accessed by choosing Help Browser...
from the
Help menu in the upper right corner of the MATHEMATICA window. An even
better way to get help is to consult an experienced MATHEMATICA user. The
Computer Lab Assistants don't usually fit into this category (but they will if
you're working in the Nielsen Hall Lab).
-
Basic Information.
- Shift-Enter sends input to MATHEMATICA.
While MATHEMATICA is compiling the input you will usually see "evaluating" at the bottom of the
screen. If "evaluating" remains there for a long time you have probably given
MATHEMATICA a problem that involves too many calculations, often you can
interrupt the calculation with Alt-+ .
Or you can choose "Abort Evaluation" from the "Kernel" menu.
(Note: Alt-+ means to simultaneously hold down the
Alt and + keys.
Likewise Shift-Enter indicates simultaneously pressing
the Shift and Enter
keys.)
- Return (or
Enter) starts a new line on your screen but DOES NOT
invoke MATHEMATICA. Use this to keep your lines from scrolling too far
to the right, epecially if you are planning to make a print-out of your session.
- Commands and functions always start with a capital letter.
Arguments are enclosed in square brackets " [ ]",
not parentheses. For example, try compiling the command
Log[1] or
ArcSin[1]. Then, for comparison,
compile the commands
Log(1) and
ArcSin(1).
- Parentheses
(round brackets " ( )") should be used to make sure
operations work as desired. For example, compare the outcome of
1/2 * 2 with 1/(2 * 2).
- The percent sign % can be used as a shorthand
to denote the last result generated, and %% is the
second-to-last result. On the other hand,
%7 would represent the output result in the output
line number 7, and so on.
- For WINDOWS users: If previous text is blocked off using the mouse it can be
copied using Control-c
and then Control-v ,
after repositioning the cursor where you want to insert the blocked text.
- A semi-colon " ; " at the end
of a line will suppress the MATHEMATICA output. (So MATHEMATICA does the computation but doesn't
print it to the screen.)
-
Elementary Functions.
- Either x * y or
x y (with a blank space inserted
between x and y) denotes multiplication of x by y. If you write
xy without a space
between the x and y then MATHEMATICA will attempt to interpret this as
a variable name (and it will NOT interpret it as multiplication).
However you can, for example, write 5x
to denote 5 * x , but
x5 will again be interpreted as a variable name.
- For exponents, write x^7
for x7, and so on.
- The common constants
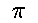 and
e are denoted by Pi and
E respectively in MATHEMATICA.
and
e are denoted by Pi and
E respectively in MATHEMATICA.
- Basic elementary functions are invoked by Sin[x], Cos[x],
Sinh[x], Sec[x], Tan[x], ArcSin[x], ArcTan[x], Sqrt[x], Log[x], Exp[x], and etc.
(The interpretations should be obvious. Note that Log[x]
is the natural logarithm function ln(x).)
- Write N[ Sqrt[2] ] to get an approximation to
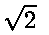 ,
or N[ Sqrt[2] , 30 ] to get an approximation accurate to
30 decimal places.
,
or N[ Sqrt[2] , 30 ] to get an approximation accurate to
30 decimal places.
-
Algebra and Calculus.
Try having MATHEMATICA compile each of the following to see what
happens:
- Expand[ (x+y+z)^2 ]
- Factor[ x^3 + 2x^2 - 5x - 6 ]
- Simplify[ Sin[x]^2 + Cos[x]^2 ]
- Integrate[ x^5 * Sin[x] , x ]
- NIntegrate[ E^(x^2), {x, 0, 3} ]
(This numerically approximates the definite integral
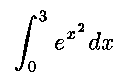 .)
.)
- D[ Log[x] * Sin[x], x ]
(This computes the derivative with respect to x.)
- D[ Log[x] * Sin[x], {x,3} ]
(This computes the third derivative with respect to x.)
- Solve[ x^2 + x - 1 == 0, x ]
(Note: == is a doubled equal sign, its always used for Logical Equality.)
- Limit[ Sin[x]/x, x --> 0 ]
(So MATHEMATICA knows how to apply L'Hospital's Rule!)
-
Fundamentals of Graphing.
Try having MATHEMATICA compile each of the following to see what
happens:
- Plot[ Cos[x^2] , {x,-Pi,Pi} ]
This gives the graph of y=cos(x2) on the interval
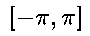 . You can get MATHEMATICA to
enlarge the picture by first clicking on the graphic output and then
dragging one of the little black rectangles while holding down the left
mouse button.
. You can get MATHEMATICA to
enlarge the picture by first clicking on the graphic output and then
dragging one of the little black rectangles while holding down the left
mouse button.
- Plot[ Cos[ x^2 ] , {x, -Pi, Pi},
PlotRange -> { 0,1 } ]
- Plot[ Cos[ x^2 ] , {x, -Pi, Pi},
AxesLabel -> {"x-axis", "y-axis"},
Frame -> True, PlotLabel -> {"My graph"} ]
- Plot3D[ x^2 - y^2 , {x, -3, 3}, {y,-3,3}]
More details on controlling the output of the "Plot"
command can be found on the 2-dimensional plotting page.
Graphing functions of two variables is discussed on the
"Plot3D" command page.
URL: http://math.ou.edu/~amiller/math/mathint.htm
August 23, 2000


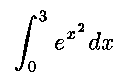 .)
.)
