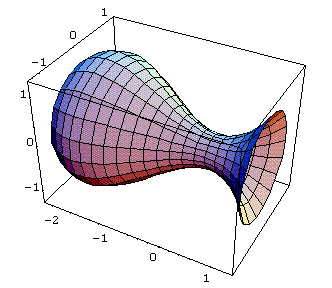
The "ParametricPlot3D" command in MATHEMATICA

The basic command in MATHEMATICA for sketching the graph of a surface described by parametric equations is:

ParametricPlot3D[ {f(u,v), g(u,v), h(u,v)}, {u,umin,umax}, {v,vmin,vmax} ]

This will sketch the surface with parametric equations

        x = f(u,v)
        y = g(u,v)
        z = h(u,v)

as (u,v) ranges through the rectangle [umin,umax] × [vmin,vmax] in the uv-plane. For example the output of

ParametricPlot3D[ {u, Sin[v]*(u^3+2u^2-2u+2)/5, Cos[v]*(u^3+2u^2-2u+2)/5}, {u,-2.3,1.3}, {v,0,2Pi}]

is the surface of revolution:

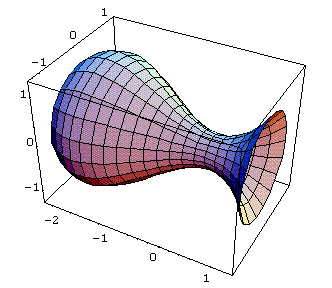
and the output of

ParametricPlot3D[ {Sin[u]Cos[v], Cos[u]Cos[v], Sin[v]}, {u,0,Pi}, {v,-Pi,Pi} ]

is the unit sphere centered at the origin:

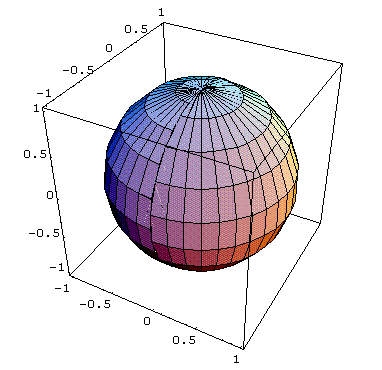
Here is a table of some modifiers which can be used.

AmbientLight -> RGBColor[NN,NN,NN]	change color of the surface
Axes -> BB	include or omit axes
Background -> RGBColor[NN,NN,NN]	create a colored background
Boxed -> BB	include or omit box around figure
BoxRatios -> {NN, NN, NN}	specify the ratios of side lengths of the box (like setting the aspect ratio for a window)
Lighting -> BB	use simulated lighting or not
PlotLabel -> "TEXT"	create a label for the contour plot
PlotPoints -> NN	number of points in each direction to sample. Raising this number will give a more accurate picture.
SphericalRegion -> BB	this will keep the size of box constant when you change viewpoint
ViewPoint -> {NN,NN,NN}	coordinates of point from which to view box

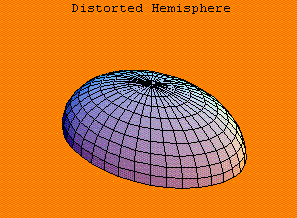
In this table, NN denotes a numerical value ( for RGBColor, the numbers NN should be between 0 and 1 ). The symbol BB takes one of the values True or False. To illustrate:

ParametricPlot3D[ {Sin[u]Cos[v], Cos[u]Cos[v], Sin[v]}, {u,0,Pi}, {v,0,Pi}, Axes -> False, Boxed->False, BoxRatios->{3,2,1}, Background -> RGBColor[1,.5,0], PlotLabel -> "Distorted Hemisphere"]

will produce the graph:

To take more control of the coloring of the surface one can try using a variation on the basic ParametricPlot3D command:

Plot3D[ {f,g,h,SS} , {u,umin,umax}, {v,vmin,vmax} ]

which will draw the parametrized surface over the rectangle [umin,umax] × [vmin,vmax] in the uv-plane, and with shading controlled by SS. To make this work you will also need to set Lighting -> False. For example,

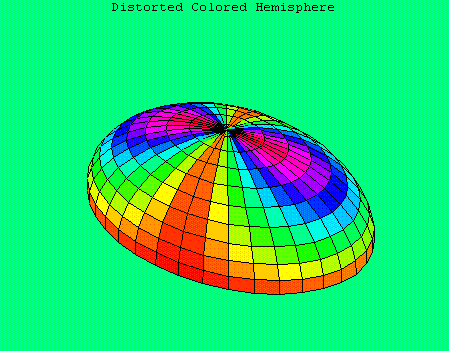
ParametricPlot3D[ {Sin[u]Cos[v], Cos[u]Cos[v], Sin[v], Hue[Sin[v]*Sin[u]]}, {u,0,Pi}, {v,0,Pi}, Axes -> False, Boxed->False, BoxRatios->{3,2,1}, Lighting -> False, PlotLabel -> "Distorted Colored Hemisphere", ViewPoint->{1,-2,2}, Background -> RGBColor[0,1,.5] ]

sets the colors on the graph as a function of sin(v)sin(u):

URL: http://math.ou.edu/~amiller/math/pplot3d.htm

August, 1999