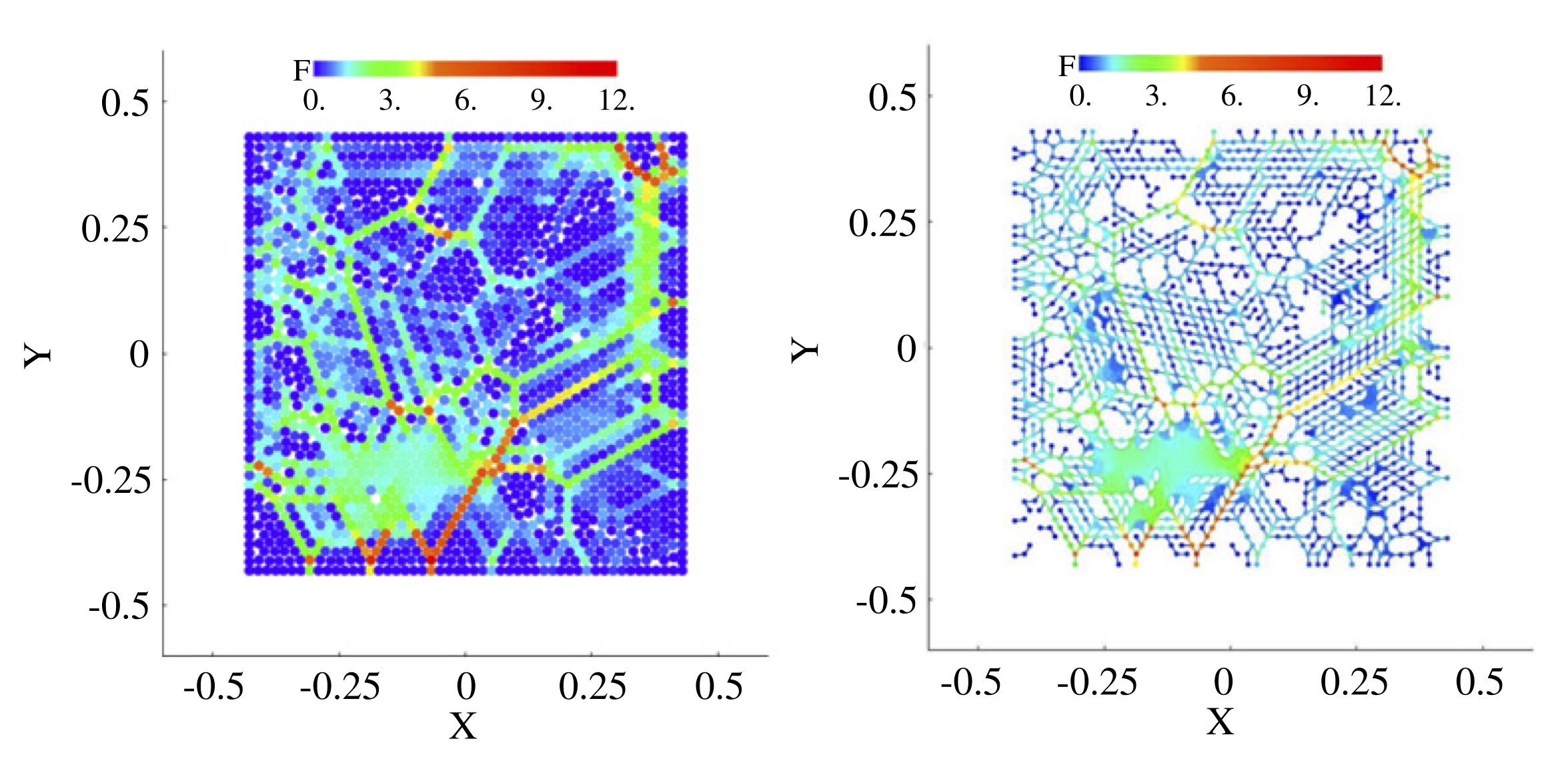
---

---

---

It is known that many granular systems are composed of particles that remain in contact for relatively long periods. These contacts can be modeled as links in a network of particles. However, this contact network provides only partial information about the interaction between the particles. Forces propagating through the material tend to create filamentary structures known as force chains.   The properties of force chains are of fundamental importance for the purpose of revealing the underlying physical causes of many phenomena. Therefore, describing and eventually understanding their properties is of significant interest. We discovered that analysis of the force chains via persistent homology of a digital image can be misleading because it is sensitive to small experimental errors in the data. Thus, in [1], we developed force networks, which are stable with respect to small perturbations and provide a more robust framework for the analysis.

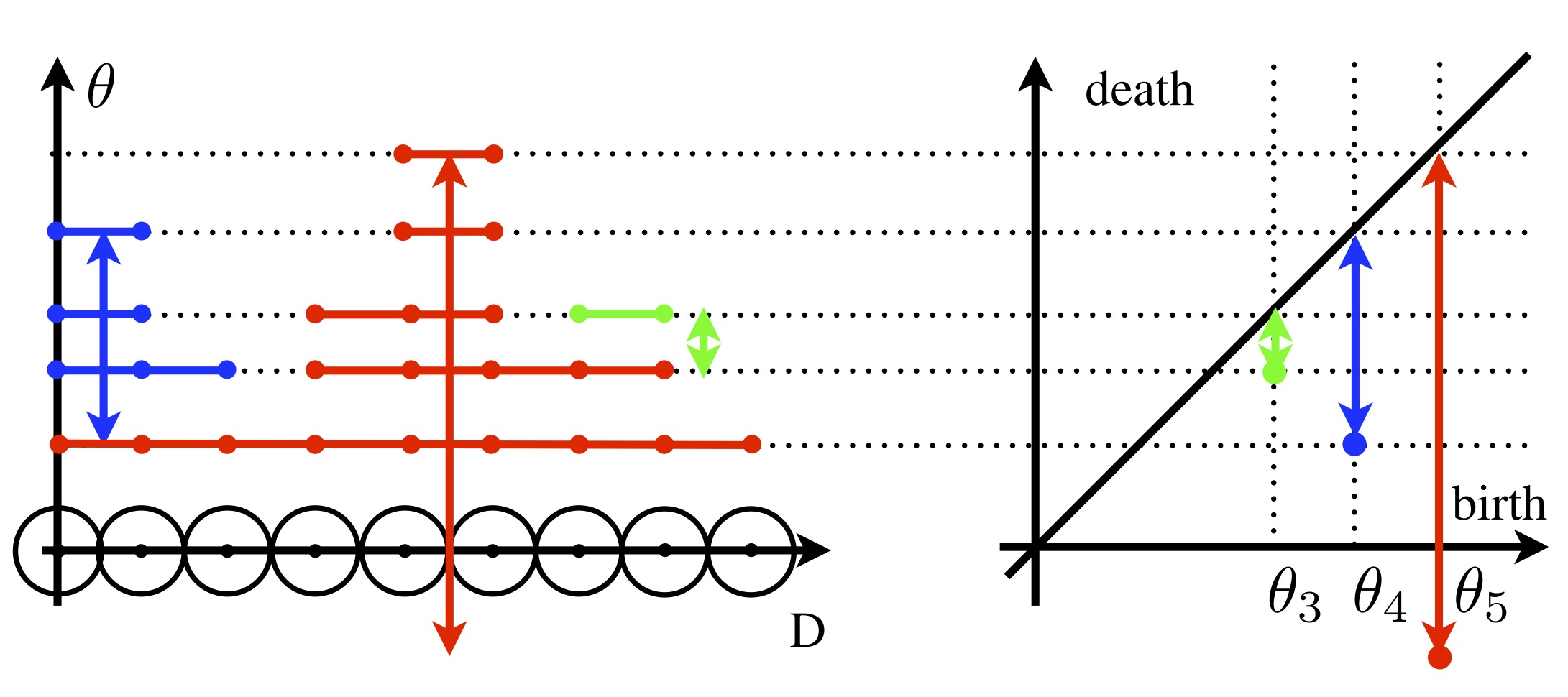
Relevant physical systems consist of large numbers of particles, and their force networks are highly complex. Due to this complexity, it is necessary to devise techniques that can capture only the important features of these networks while disregarding unimportant details. In our work, we developed a compact but informative description of force networks that can be efficiently computed for large systems [1]. In particular, we use persistence diagrams to obtain a global description of the network. Persistence diagrams succinctly encode the geometric features of the network, such as distinct connected components and holes, at all force levels.

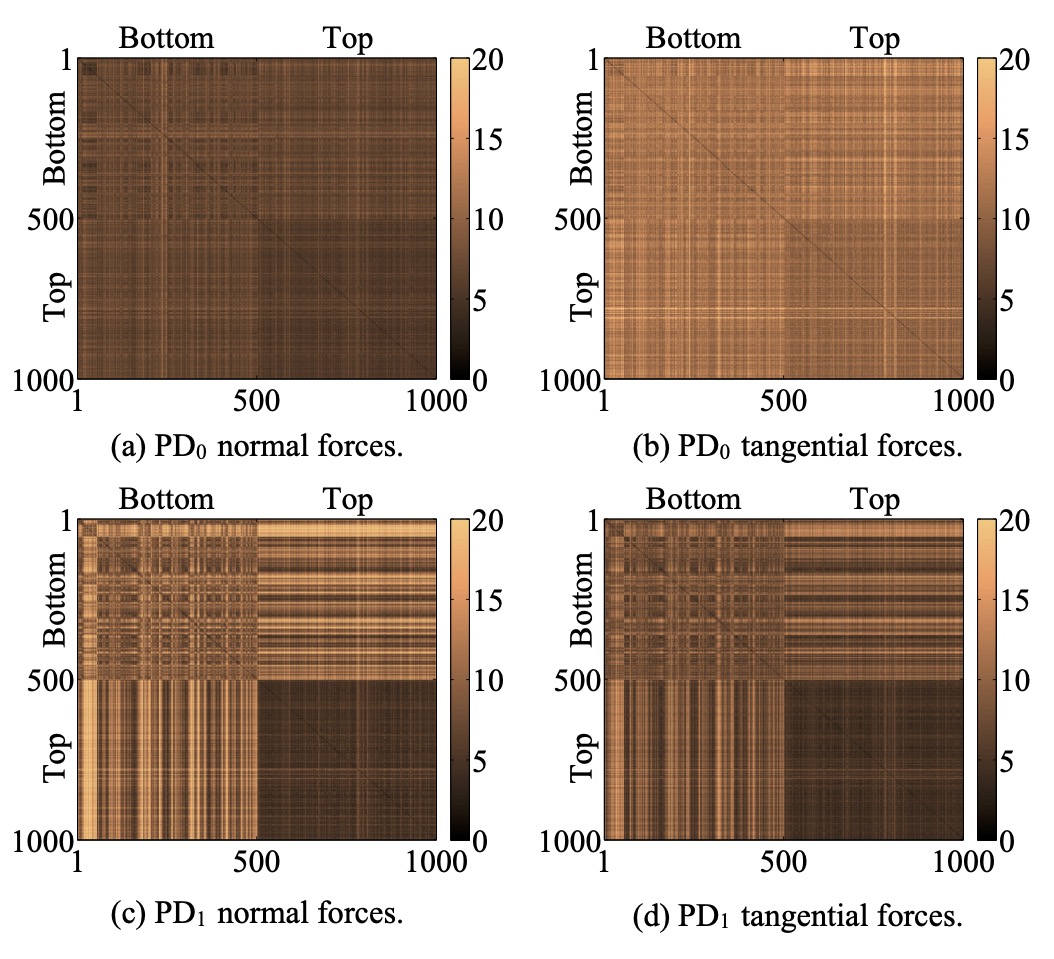
Using these methods, we were able to quantify structural differences between force chains depending on the friction coefficient and polydispersity of the system [2,3,4], as well as the shape of the particles [5,6]. We also showed that steady states with similar packing fractions, prepared by tapping a confined granular column with different intensities, can be distinguished via their force networks. Moreover, for a linearly sheared system, our work [7]  revealed differences between experimental data and simulations. It also provided insights for further model improvement and highlighted deficiencies of current methods used for force network reconstruction from experimental data.

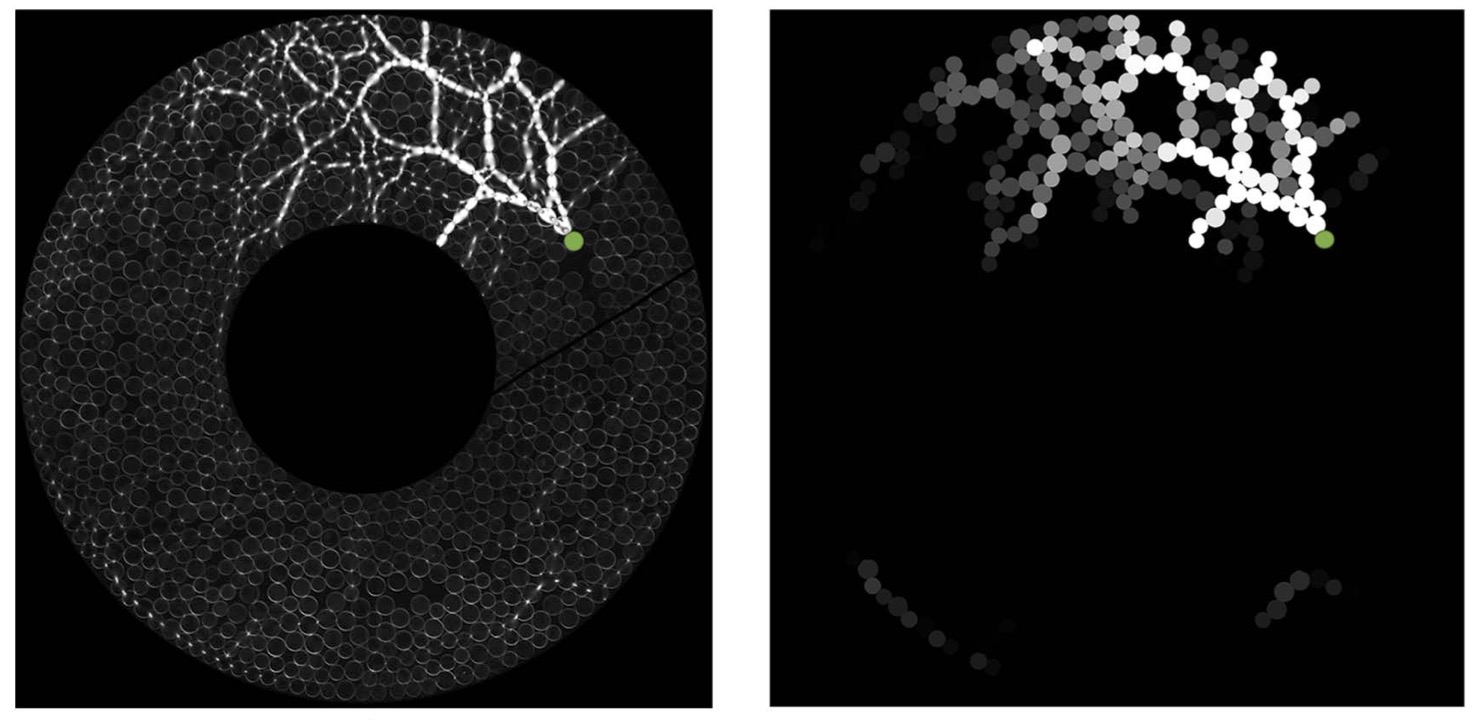
To address the lower resolution of the experimental data and the fact that the detailed structure of force networks is difficult to extract from experiments, we investigated the correlation between data containing different amounts of information [8]. We performed simulations to accurately model experiments of an intruder being pushed through a two-dimensional granular layer and compared features of the persistence diagrams describing force networks and networks constructed using only the sum of the normal forces on each grain. The main features of the networks are highly correlated, suggesting that data commonly available in experiments are sufficient to capture the most prominent structures of force networks in evolving granular systems. We used this approach to study the experimental data where we infer the integrated strain magnitude from the photo-elastic response of each particle [9]. The considered system undergoes a stick-slip dynamics. Our analysis reveals that force networks evolve smoothly but in a nontrivial manner throughout each stick period, even though the intruder and granular particles are stationary.