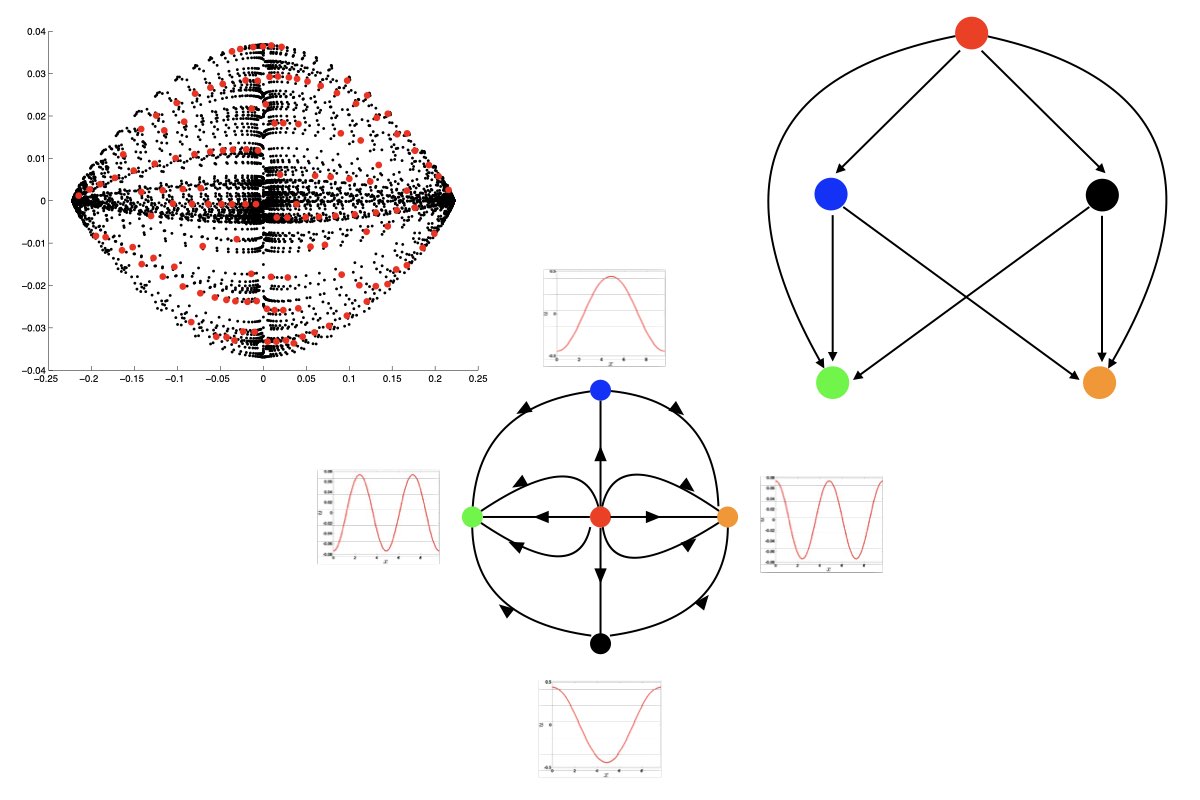
---

---

Analytical methods help study the dynamics of mathematical models, but their applicability to data is often limited. The primary limitations stem from the finite nature of the data and the presence of noise. Topological ideas can help reduce the dimension and cope with noise. For example, the Conley index can be used to show the existence of fixed points, periodic orbits, and other invariant sets hidden in the experimental data.

Another significant advantage of topological methods is that complete information about the flow is not required. It is sufficient to construct its outer approximation, which describes the flow only up to a particular spatial scale. Naturally, this does not allow us to detect all invariant sets, but the detected invariant sets are guaranteed to exist. The description of the dynamics exhibited by the system becomes finer with the increase of available information about the flow.

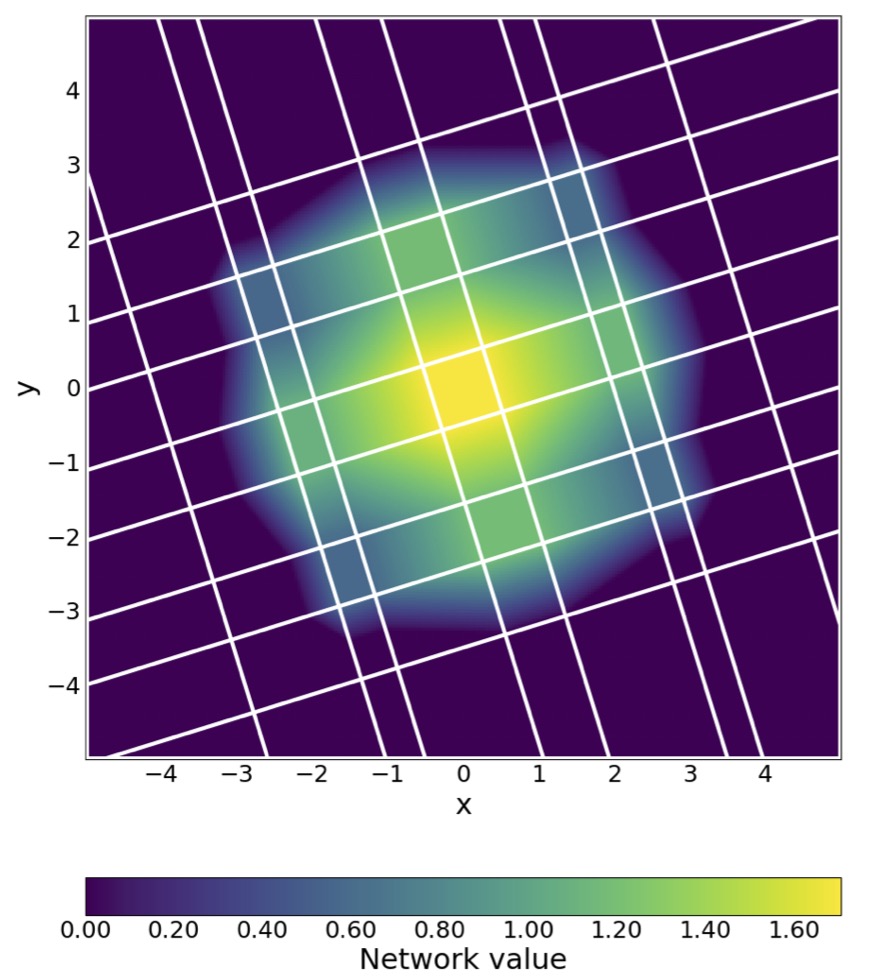
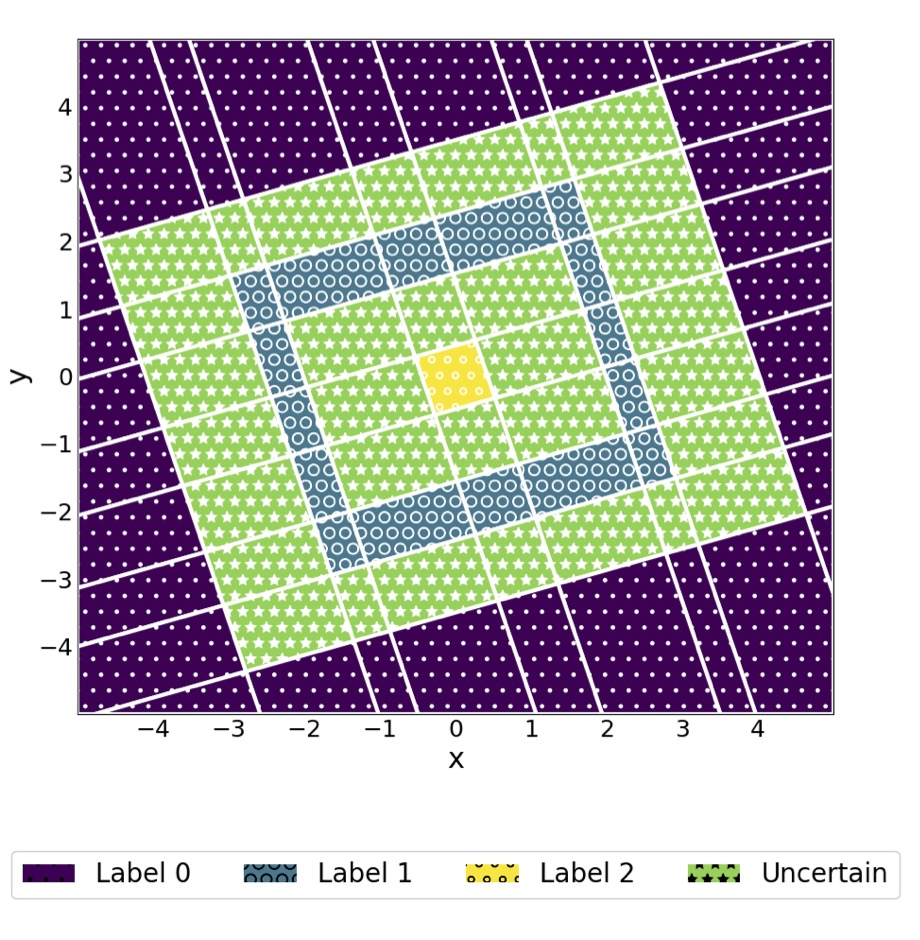
The construction of an outer approximation of the system consists of two steps. First, a tessellation of the phase space with the required resolution is constructed. Then, the outer approximation is defined as a combinatorial multivalued map that captures the dynamics at the spatial resolution given by the size of the tiles. This construction can be carried out using a cubical grid, but it may contain too many cubes.

Recently, we have been exploring possibilities to reduce the size of the grids necessary to produce relevant descriptions of the dynamics, such as the Morse graph and Conley indices of the Morse sets. Our novel approach uses machine learning to discover the grid. The neural network that produces the grid is trained on sampled trajectories of the system [1]. Even if the system's underlying equations are unknown, these samples can be obtained from experiments.

Regardless of the particular tessellation described above, the dimensions of the grid elements and the ambient space are equal. Thus, the curse of dimensionality often makes it impossible to perform the computations, even if the interesting dynamics is low dimensional. To avoid this problem, one can apply the above machinery only to the system's attractor. The dimension of the attractor is much smaller than the dimension of the ambient space, but its structure is much more complicated. Currently, we are investigating the possibility of representing the attractor by a collection of lower dimensional facets of a cubical grid. The idea is to ensure that most facets' dimensions are comparable to the manifold's intrinsic dimension. The rigidity of the cubes makes them well-suited for efficient computations on a computer.