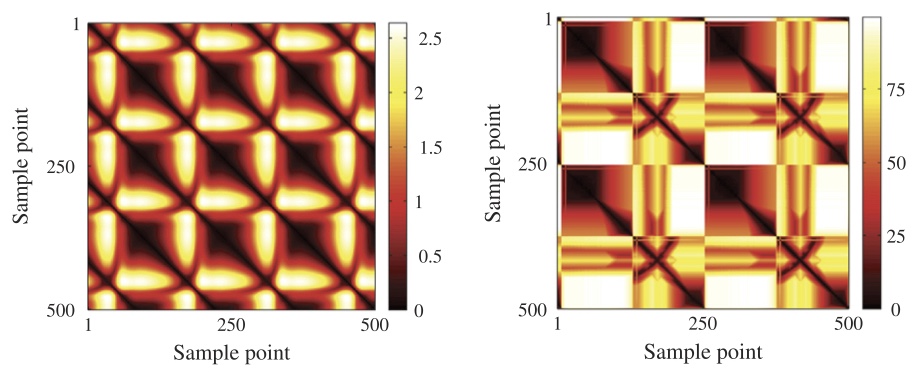
---

---

Our research introduces a novel application of persistent homology in the analysis of fluid motion patterns. To visualize the fluid motion, we employ a technique called shadowgraph photography. The dark (light) pixels correspond to the fluid flowing downward (upward). In this case, we directly apply persistent homology to the scalar function defined by the gray scale values of the pixels.

Complex spatio-temporal systems often exhibit complicated pattern evolution, which can be succinctly described by persistent homology [1]. By applying different metrics to the space of persistence diagrams, we relate characteristic features in persistence diagrams to the geometry of the corresponding flow patterns. We also examine the dynamics of the flow patterns by a second application of persistent homology to the time series of persistence diagrams. Our research demonstrates that persistent homology provides an effective method both for quotienting out symmetries in families of solutions and for identifying multiscale recurrent dynamics. We have shown how persistent homology can identify equilibria and periodic dynamics. This method is particularly natural when solutions on a group orbit must be identified.

Substantial insight into the dynamics and statistics of chaotic systems can be obtained from unstable time-periodic solutions of the governing equations. Chaotic dynamics follow, or shadow, such solutions transiently and repeatedly. Therefore, detecting shadowing events is essential for prediction and control. Conceptually, the most straightforward approach to detecting shadowing relies on computing the Euclidean distance to one of the unstable solutions in state space. This approach becomes computationally inefficient for spatially extended systems where unstable solutions come in continuous families related to the associated translation and/or rotation symmetries. We propose [2] to detect shadowing in the space of persistence diagrams, which provides a symmetry-invariant representation. We show that the two approaches yield consistent results for the Kuramoto-Sivashinsky equation. However, our approach is computationally efficient and can be used for higher dimensional systems with several symmetries. We show that the asymptotic complexity of the proposed method remains the same as the number of continuous symmetries grows and is much lower than for the classical approach.