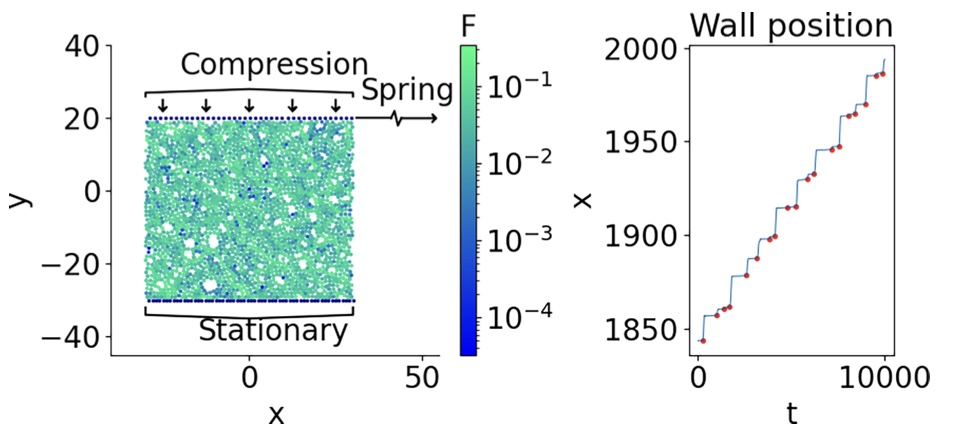
---

---

---

If a system of granulate particles is exposed to externally applied time-dependent shear stress, it often produces intermittent stick-slip dynamics. In this regime, the top wall confining the particles remains almost at rest until the stress applied to it becomes sufficiently large and the wall slips. Understanding the intermittent stick-slip dynamics is of utmost importance because of its relevance to large-scale, possibly cataclysmic events such as earthquakes. For obvious reasons, there is an active interest in identifying precursors to the slip events that lead to abrupt structural rearrangements of the systems. Despite much work on identifying the precursors of slip events, their use for predictive purposes needs to be improved.

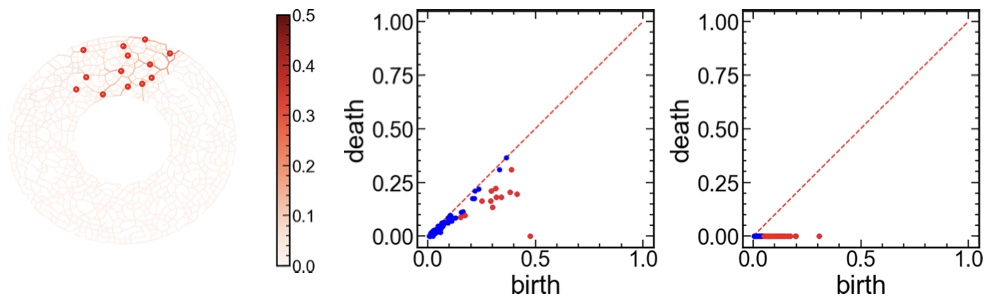
In our work [1], we compared two groups of measures describing the behavior of the system. The first group consists of global measures defined as system-wide averages at a fixed time. These measures are not sensitive to an approaching slip event. The second group consists of time-dependent measures that quantify the system's evolution on a micro (particle) or mesoscale. Measures in this group first quantify the temporal differences between two states and only then aggregate them to a single number. The behavior of the measures in the second group changes dramatically before a slip event starts. They increase rapidly as a slip event approaches, indicating a significant increase in fluctuations before a slip event is triggered. We hypothesize that the intensity of the fluctuations in the system increases until it overcomes the stabilizing effects of the force network and triggers a slip event. Therefore, information about the system's evolution on micro and mesoscopic scales seems vital for accurately predicting the occurrence of a slip. Even in the coarser experimental data for the intruder system, we found characteristic features of persistence diagrams that provide identifiable slip precursors [2].

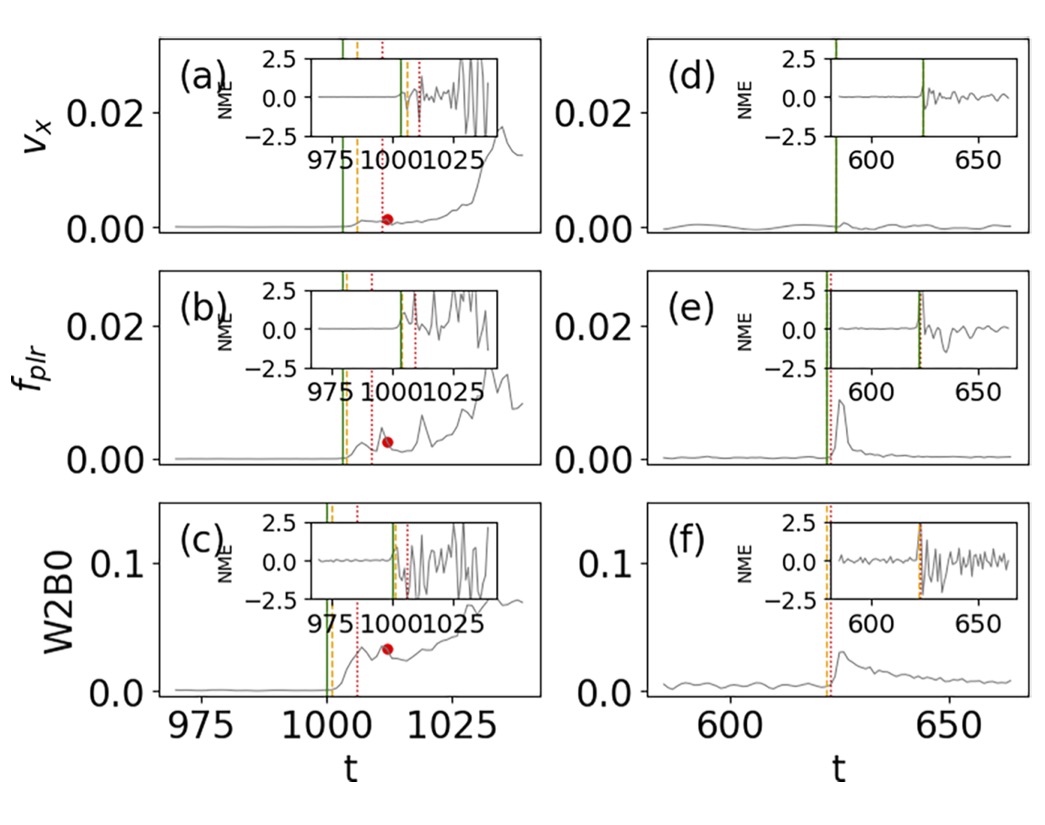
Using these time-dependent measures, we can predict upcoming slip events using stochastic state space models [3]. We show that the measures describing the forces between the particles provide earlier detection of a forthcoming slip event than those based solely on the wall movement. By comparing the detection times obtained from the considered measures, we observe that a typical slip event starts with a local change in the force network. However, some local changes do not spread globally over the force network. For the changes that become global, we find that their size strongly influences the further behavior of the system. If the size of a global change is large enough, it triggers a slip event; if it is not, then a much weaker microslip follows.

The system's sensitivity to small perturbations strongly influences the longest time horizon on which reasonable predictions can be made. In particular, the history dependence of the evolution of complex systems plays a vital role in forecasting. The predictions' precision declines as the systems' memory is lost. In [4], we developed a simple method for assessing the rate of memory loss applicable to experimental data. This rate indicates how fast future states become independent of the initial condition. Under certain regularity conditions on the invariant measure of the dynamical system, we prove that our method provides an upper bound on the mixing rate of the system. This rate can be used to infer the longest time scale on which the predictions are still meaningful.