
Sarah Day, William Kalies, Thomas Wanner, Verified Homology Computations of Nodal Domains Multiscale Model. Simul. 7 (2009)
An algorithm for approximating a nodal domain by a cubical complex with the same homology was introduced in Verified Homology Computations of Nodal Domains. We improved and extended this algorithm to higher dimensions. We also exploited the nonuniformity of the grid to reduce the memory requirements for computing the homology.
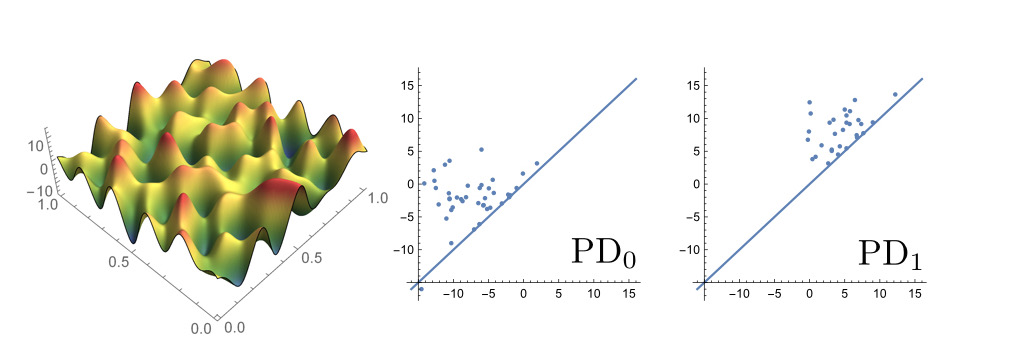
J. Jaquette and M. Kramar, Rigorous Computation of Persistent Homology, arXiv:1412.1805, (2015).
Recent developments in topological data analysis clearly show the power of persistent homology. Therefore we devised an algorithm for computing the persistence diagrams of C1 functions defined on an N-dimensional cube. For a given function and a chosen tolerance value T we prove that the bottleneck distance of the computed and real persistence diagrams is less than T.
Another important application of persistent homology is capturing geometry of the point clouds. This is usually done by computing persistence diagrams for alpha shape complex (in R3), witness complexes (in Rn) or Vietoris-Rips complex (in general metric space). Persistence diagrams corresponding to large point clouds, usually cannot be computed because of the memory constrains. Therefore, we developed and algorithm that computes an adaptive approximation of the diagram. The error tolerance is allowed to change with a threshold in such a way that the computations can be performed using the available resources.