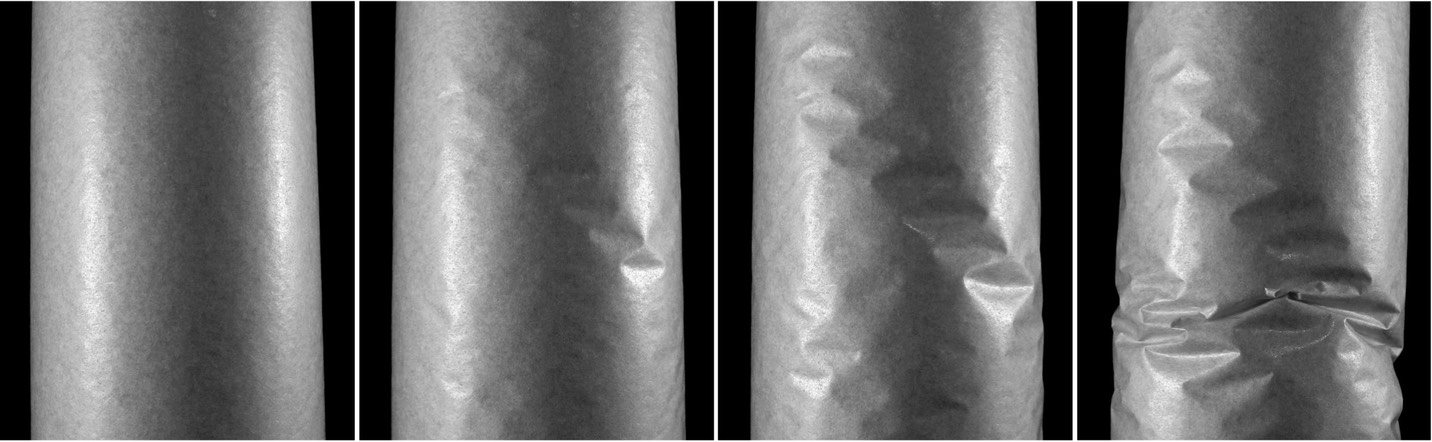
Collapse under granular discharge. Courtesy of Claudia Colonnello.
We are studying time evolution of the local deformations of paper silos during their discharge. If the silo is loaded above its critical threshold, then it will collapse during its discharge. The value of this threshold is not precisely known and it decreases with the age of the silo. We use persistence diagrams to describe deformations of the silo. By analyzing the evolution of these deformations in the space of persistence diagrams, we are able to distinguish the collapsing and non-collapsing silos at the early stages of their discharge.
Recent development of parallel algorithms for computing persistent homology is likely to lead to the real time prediction of a collapse before it actually happens. We are trying to construct an appropriate basis which can be used to predict the behavior of the system based on its current state and/or the previously observed evolution. After building the initial basis, coordinates of the later observed states can be efficiently computed using the distance trees. I would like to apply machine learning approaches to the low dimensional representations of the phase space and devise a system that can learn to indicate the approaching collapse at the stage at which it can be prevented. In the future, I would like to apply these ideas to more complex systems.