MATH 4193.001/5093.001 - Introductory Mathematical Modeling / Mathematical Models - Spring 2013
TR 1:30--2:45 p.m., PHSC 102
Instructor:
Nikola Petrov, 802 PHSC, (405)325-4316, npetrov AT math.ou.edu
Office Hours:
Mon 9:30-10:30 a.m., Tue 2:45-3:45 p.m., or by appointment.
Check out the
OU Math Blog!
It is REALLY interesting!
Course catalog description:
For 4193: Prerequisite: 3113 or 3413, 3333, 4733 or 4753,
or permission of instructor.
Mathematics models are formulated for problems arising in various areas
where mathematics is applied. Techniques are developed for analyzing
the problem and testing validity of proposed model. (F)
For 5103: Prerequisite: permission of instructor or admission
to the M.S. program. May be repeated with change of content;
maximum credit six hours. Mathematical models are formulated
for problems arising in various areas in which mathematics has been applied.
In each case, techniques are developed for analyzing the resulting mathematical
problem, and this analysis is used to test the validity of the model. (Sp)
Text:
Steven H. Strogatz.
Nonlinear Dynamics And Chaos, with Applications to Physics,
Biology, Chemistry, and Engineering. Westview Press, 2001,
ISBN: 0738204536.
We will also use parts of the following books,
freely available online for OU students:
A. C. King, J. Billingham, S. R. Otto.
Differential Equations: Linear, Nonlinear, Ordinary, Partial.
Cambridge University Press, 2003;
R. Seydel. Practical Bifurcation and Stability Analysis.
Third ed., Springer, 2010.
A brief (tentative) list of topics to be covered:
-
One-dimensional systems:
flows on the line,
bifurcations,
flows on the circle.
-
Two (and higher)-dimensional flows:
linear systems,
the phase plane,
limit cycles,
bifurcations.
-
Chaos:
the Lorenz equations,
one-dimensional maps,
fractals,
strange attractors.
A brief description of the class:
The class will study basic theory of nonlinear dynamics.
Since a nonlinear system of ODEs does not satisfy the Superposition Principle,
finding the general solution of such a system is very complicated
and often impossible. Because of this, one can instead try to describe
the qualitative behavior of the solutions of the system.
In this class we will derive nonlinear (systems of) ODEs
occurring in some simple mechanical problems, and will analyze
the behavior of their solutions. We will discuss briefly questions
of existence and uniqueness of solutions, and will develop some methods
for studying their bifurcations, i.e., situations in which the solutions
of the system change their qualitative behavior dramatically for a small
change of some parameter. We will study the phase portraits of autonomous
linear systems, some bifurcations occurring in such systems
(saddle-node, transcritical, pitchfork, Hopf),
presence or absence of certain types of asymptotic behavior of the solutions,
relaxation oscillations, limit cycles, hysteresis, Poincaŕe aps, etc.
We will discuss the famous Lorenz system and similar systems exhibiting
highly irregular behavior ("chaos").
We will also study some concepts related to highly iterated maps,
i.e., the behavior of
) ,
where the function (”map”)
,
where the function (”map”)
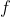 is composed with itself
is composed with itself
 times, for
times, for
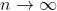 .
We will study bifurcations in some maps, their periodic orbits, Lyapunov exponents,
and the universal behavior of such maps. If time permits, we will touch on different
concepts of dimension that are important in the context of nonlinear dynamics.
.
We will study bifurcations in some maps, their periodic orbits, Lyapunov exponents,
and the universal behavior of such maps. If time permits, we will touch on different
concepts of dimension that are important in the context of nonlinear dynamics.
Homework:
-
Homework 1,
due Tuesday, February 12.
Codes needed for Homework 1:
-
Homework 2,
due Thursday, February 28.
[Note the new due date!]
-
Homework 3,
due Thursday, March 14,
in class!
-
Homework 4,
due Thursday, April 18.
-
Homework 5,
due Thursday, May 2.
Content of the lectures:
-
Lecture 1 (Tue, Jan 15):
Introduction:
Overview of the course, viewing of the NOVA documentary
"The Strange New Science of Chaos" (31 January 1989)
available on
YouTube.
On recent history, see
J. Gleick's book
Chaos: Making a new Science.
(Penguin, 1987).
-
Lecture 2 (Thu, Jan 17):
The importance of being nonlinear:
ODEs vs. PDEs,
number of arbitrary constants in the general solutions of ODEs,
arbitrariness in the general solutions of PDEs,
why is a function "equivalent" to infinitely many constants;
systems of first-order ODEs, autonomos vs. nonautonomous systems,
converting a single higher-order ODE into a system of 1st-order ODEs,
linear systems, example (harmonic oscillator with air-resistance
force and external driving force), example (pendulum);
nonlinear systems are so hard to solve because the principle
of superposition fails (hence no normal modes, no Fourier transform,
no Laplace transform...)
[Sec. 1.2]
Flows on the line - a geometric way of thinking:
showing that that the solution of the IVP (initial value problem)
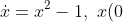=x_0) is
is
=\frac{x_0+1+(x_0-1)\mathrm{e}^{2t}}{x_0+1-(x_0-1)\mathrm{e}^{2t}},)
and studying the asymptotic
(i.e., for
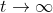 )
behavior of the solution
[Sec. 2.0, page 16 of 2.1]
)
behavior of the solution
[Sec. 2.0, page 16 of 2.1]
-
Lecture 3 (Tue, Jan 22):
Flows on the line - a geometric way of thinking (cont.):
analyzing the asymptotic behavior of the solutions of the IVP
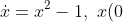=x_0) without solving the IVP, vector fields on
without solving the IVP, vector fields on
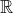 );
fixed points (FPs)
);
fixed points (FPs)
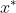 (satisfying
(satisfying
=0) ),
stable FPs (atracting FPs, attractors, sinks),
unstable FPs (repelling FPs, repellers, sources)
[Sec. 2.1]
),
stable FPs (atracting FPs, attractors, sinks),
unstable FPs (repelling FPs, repellers, sources)
[Sec. 2.1]
Fixed points and stability:
using phase portraits (plots of
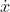 vs.
vs.
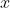 )
in order to analyze the behavior of the solutions of the system;
an example:
)
in order to analyze the behavior of the solutions of the system;
an example:
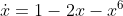 ;
an example with a half-stable (semi-stable) FP:
;
an example with a half-stable (semi-stable) FP:
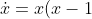^2) ,
"non-genericity" of half-stable FP.
[Sec. 2.2]
,
"non-genericity" of half-stable FP.
[Sec. 2.2]
Population growth:
simplest model of population dynamics:
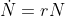 (where
(where
 is the growth rate), deficiency of the model;
improving the model to account for the limited amount of resources:
logistic equation
is the growth rate), deficiency of the model;
improving the model to account for the limited amount of resources:
logistic equation
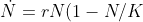) (where
(where
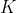 is the carrying capacity of the ecosystem),
stability of the FPs of the logistic equation,
deficiencies of the logistic model
[Sec. 2.3]
is the carrying capacity of the ecosystem),
stability of the FPs of the logistic equation,
deficiencies of the logistic model
[Sec. 2.3]
Linear stability analysis:
the time evolution a small perturbation
=x(t)-x^*) of the solution
of the solution
) of the ODE
of the ODE
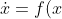) about the fixed point
about the fixed point
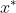 is governed by the linearization
is governed by the linearization
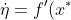\eta) of the ODE about the fixed point
of the ODE about the fixed point
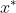 [pages 24-25 of Sec. 2.4]
[pages 24-25 of Sec. 2.4]
-
Lecture 4 (Thu, Jan 24):
Linear stability analysis (cont.):
examples of linear stability analysis and its failures
[pages 25-26 of Sec. 2.4]
Existence and uniqueness of solutions of ODEs:
an example of an ODE without a solution:
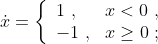
an example of an ODE with infinitely many solutions:
formation and growth of a droplet in an oversaturated vapor
[Sec. 2.5]
Impossibility of oscillations:
monotonicity of the approach to a stable equilibrium
in a single autonomous ODE implies impossibility of oscillatory
solutions; topological arguments for impossibility
of certain configurations of fixed points on
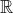 ;
mechanical analog - overdamped systems
[Sec. 2.6]
;
mechanical analog - overdamped systems
[Sec. 2.6]
Potentials:
potential of a first-order system;
each function
) admits a potential:
admits a potential:
=-\textstyle{\int_0^x} f(s)\,\mathrm{d}s) (not true in general for functions of more variables);
the potential decreases along trajectories, examples
[Sec. 2.7]
(not true in general for functions of more variables);
the potential decreases along trajectories, examples
[Sec. 2.7]
Solving equations on the computer:
Euler's method for solving IVPs for ODEs numerically
[pages 32-33 of Sec. 2.8]
Saddle-node bifurcation:
occurrence (disappearance) of a pair of fixed points
of opposite stability for the system
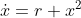 [page 45 of Sec. 3.1]
[page 45 of Sec. 3.1]
-
Lecture 5 (Tue, Jan 29):
Saddle-node bifurcation (cont.):
occurrence of a saddle-node bifurcation in the system
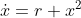 ,
graphical representation,
examples, normal forms, conversion to a normal form near a bifurcation
by using Taylor expansion of the right-hand side of the ODE
[Sec. 3.1]
,
graphical representation,
examples, normal forms, conversion to a normal form near a bifurcation
by using Taylor expansion of the right-hand side of the ODE
[Sec. 3.1]
Transcritical bifurcation:
occurrence of a transcritical bifurcation in the system
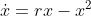 (in which a fixed point changes its stability), examples
[Sec. 3.2]
(in which a fixed point changes its stability), examples
[Sec. 3.2]
-
Lecture 6 (Thu, Jan 31):
Pitchfork bifurcation:
supercritical pitchfork bifurcation in the system
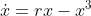 ,
spontaneous magnetization in a magnetic material
[pages 55-58 of Sec. 3.4]
,
spontaneous magnetization in a magnetic material
[pages 55-58 of Sec. 3.4]
-
Lecture 7 (Tue, Feb 5):
Pitchfork bifurcation (cont.):
subcritical pitchfork bifurcation in the system
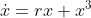 ;
demonstration that the coefficients
;
demonstration that the coefficients
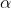 and
and
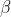 in the system
in the system
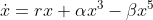 can be eliminated by a change of the function
can be eliminated by a change of the function
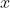 and the "time"
and the "time"
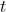 by constant factors,
bifurcation analysis of the system
by constant factors,
bifurcation analysis of the system
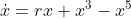 ,
jumps and hysteresis [pages 58-60 of Sec. 3.4]
,
jumps and hysteresis [pages 58-60 of Sec. 3.4]
Insect outbreak:
derivation of a system modeling the dynamics of the budworm
population accounting for the limited resources and the predation:
-p(N) \ \mbox{ for } \ p(N)=\frac{BN^2}{A^2+B^2}\,;)
non-dimensionalizing the problem [pages 73-75 of Sec. 3.7]
-
Lecture 8 (Thu, Feb 7):
Insect outbreak (cont.):
a complete analysis of the bifurcations in the dynamics of budworm
population described by the equation
-\frac{BN^2}{A^2+B^2}\,;)
conditions for existance of a bistable region, cusp catastrophe,
calculations in Mathematica
saved as a
pdf file
[pages 77-79 of Sec. 3.7]
-
Lecture 9 (Tue, Feb 12):
Flows on the circle - examples and definitions:
differences between the real line and the circle,
differential equations on the circle, examples of differential
equations with fixed points, uniform oscillator
[Sec. 4.0, 4.1, 4.2]
Nonuniform oscillator:
bifurcations in the system
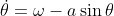 ,
linear stability analysis of the fixed points
in the case
,
linear stability analysis of the fixed points
in the case
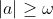 ,
exact and approximate calculations of the period of the system
for
,
exact and approximate calculations of the period of the system
for
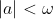 ,
square-root scaling law
[pages 96-99 of Sec. 4.3]
,
square-root scaling law
[pages 96-99 of Sec. 4.3]
-
Lecture 10 (Thu, Feb 14):
Nonuniform oscillator (cont.):
ghosts (saddle-node remnants) leading to a slow passage
through a bottleneck, rough estimates on the time of passage
through a bottleneck (and the period in such a case)
[pages 99-100 of Sec. 4.3]
Overdamped pendulum:
derivation of the exact and the approximate equations
describing the dynamics of an overdamped pendulum in the gravity field
subjected to a constant torque
[Sec. 4.4]
Definition and examples of two-dimensional linear systems:
two dimensional constant-coefficient linear systems,
phase plane; example - harmonic oscillator;
fixed points, closed orbits; determining the shape of the closed
orbits in the phase plane by using conservation of energy
- multiplying the equation of motion,
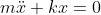 by
by
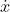 and integrating to obtain
and integrating to obtain
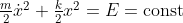 [pages 123-126 of Sec. 5.1]
[pages 123-126 of Sec. 5.1]
-
Lecture 11 (Tue, Feb 19):
Definition and examples of two-dimensional linear systems (cont.):
detailed analysis of the linear system
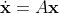 ,
for
,
for
) :
stable nodes, stars, a line of fixed points, saddle points;
stable and unstable manifolds of a saddle point;
attracting FP, globally attracting FP,
Lyapunov stable FP, neutrally stable FP (Lyapunov stable but not
attracting), (asymptotically) stable FP (both Lyapunov stable and
attracting)
[pages 126-129 of Sec. 5.1]
:
stable nodes, stars, a line of fixed points, saddle points;
stable and unstable manifolds of a saddle point;
attracting FP, globally attracting FP,
Lyapunov stable FP, neutrally stable FP (Lyapunov stable but not
attracting), (asymptotically) stable FP (both Lyapunov stable and
attracting)
[pages 126-129 of Sec. 5.1]
Classification of linear systems:
eigenvectors, eigenvalues, and their role in constructing the general
solution of a linear system of ODEs, characteristic equation,
trace and determinant of a
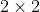 matrix
[pages 129-133 of Sec. 5.2]
matrix
[pages 129-133 of Sec. 5.2]
-
Lecture 12 (Thu, Feb 21):
Classification of linear systems (cont.):
complex eigenvalues - stable spirals, centers, unstable spirals;
equal eigenvalues - star nodes
(
 diagonalizable),
degenerate nodes
(
diagonalizable),
degenerate nodes
( non-diagonalizable);
classification of fixed points in the
non-diagonalizable);
classification of fixed points in the
) -plane
[pages 133-138 of Sec. 5.2]
-plane
[pages 133-138 of Sec. 5.2]
Phase portraits:
general systems of ODEs in the plane:
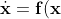) ;
flow of a differential equation - the solution of
the initial-value problem
;
flow of a differential equation - the solution of
the initial-value problem
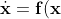) ,
,
=\mathbf{y}) :
the particular solution can be written as
:
the particular solution can be written as
) ;
properties of the map
;
properties of the map
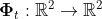 :
:
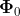 is the identity in
is the identity in
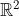 ;
;
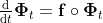 [page 145-146 of Sec. 6.1]
[page 145-146 of Sec. 6.1]
-
Lecture 13 (Tue, Feb 26):
Phase portraits (cont.):
important objects in the phase plane - fixed points, periodic
solutions (closed orbits);
important questions - arrangements of trajectories near fixed points
and closed orbits, stability of fixed points and closed orbits;
an example of calculation of a one-parameter semigroup
for a particular system of ODEs;
nullclines, an example [pages 146-148 of Sec. 6.1]
Fixed points and linearization:
linearizing a nonlinear system around a fixed point
[pages 150-151 of Sec. 6.3]
-
Lecture 14 (Thu, Feb 28):
Fixed points and linearization (cont.):
an example of linearization when the linearized system reflects
correctly the behavior of the full system around a fixed point (Example 6.3.1),
an example of linearization when the linearized system does not reflect
correctly the behavior of the full system around a fixed point
(Example 6.3.2);
robust cases (repellers, attractors, saddles) and marginal cases
(centers, higher-order and non-isolated FPs);
hyperbolic fixed points, an idea of the Hartman-Grobman Theorem,
topological equivalence of systems, structural stability of a phase
portrait;
an example of structural stability/instability in the problem of
the number of zeros of a function
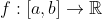 [pages 151-155 of Sec. 6.3]
[pages 151-155 of Sec. 6.3]
-
Lecture 15 (Tue, Mar 5):
Rabbits versus sheep:
modeling a system with two species competing for food,
Lotka-Volterra model of competition,
linearizations around the FPs of the system,
stable and unstable manifold of the saddle point,
basin of attraction of a FP, basin boundary, separatrices,
global phase portrait of the Lotka-Volterra system
[Sec. 6.4]
More on the Hartman-Grobman Theorem:
solution of the system
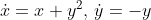 and its linearization around (0,0), explicit construction of the
conjugacy (i.e., change of variables) between the nonlinear system and
its linearization:
and its linearization around (0,0), explicit construction of the
conjugacy (i.e., change of variables) between the nonlinear system and
its linearization:
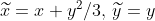 :
in these coordinates the original system becomes
:
in these coordinates the original system becomes
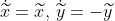 .
.
-
Lecture 16 (Thu, Mar 7):
Conservative systems:
conserved quantities, conservative systems,
dissiparion of energy in the presence of resistance forces,
conservative systems cannot have attracting FPs,
an example of a particle moving in a double-well potential (Example 6.5.2),
homoclinic connections, heteroclinic connections,
energy surface, theorem on nonlinear centers for conservative systems
(Theorem 5.6.1)
[Sec. 6.5]
Pendulum:
equation of motion of a pendulum, non-dimensionalizing
the equation of motion, the phase space of the pendulum
is an infinite cylinder
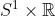 ;
representing the cylinder in the plane
[pages 168, 169, 171 of Sec. 6.7]
;
representing the cylinder in the plane
[pages 168, 169, 171 of Sec. 6.7]
-
Lecture 17 (Tue, Mar 12):
Pendulum (cont.):
linearizing the equation of the pendulum around the two fixed points,
using energy conservation to plot the phase portrait,
types of orbits of the pendulum, effects of the damping
[pages 169, 170, 172, 173 of Sec. 6.7]
Limit cycles:
definition and examples of limit cycles
[Sec. 7.0, 7.1]
Ruling out closed orbits:
gradient systems,
impossibility of closed orbits in gradient systems
[page 199 of Sec. 7.2]
-
Lecture 18 (Thu, Mar 14):
Ruling out closed orbits (cont.):
examples of application of using energy dissipation
to prove impossibility of periodic orbits;
Lyapunov functions, examples;
Dulac's Criterion for ruling out periodic orbits,
proof (using Greene's Theorem)
[Sec. 7.2]
-
Lecture 19 (Tue, Mar 26):
Poincare-Bendixson Theorem:
statement of the Poincare-Bendixson Theorem on existence of closed
orbits in planar systems of ODEs in a closed bounded domain
R⊂R2,
construction of a trapping region
(guaranteeing the existence of a trajectory that is "confined"
in the domain R),
Example 7.3.1, no chaos in the phase plane
[pages 203-205, 210 of Sec. 7.3]
Saddle-node, transcritical, and pitchfork bifurcations in
R2:
"one-dimensional" bifurcations in two-dimensional systems;
a "ghost" remaining after the disappearance of the fixed points
in a saddle-node bifurcation;
supercritical pitchfork bifurcation in two dimensions
in a prototypical example (Example 8.1.2)
[pages 241, 242, 246 of Sec. 8.1]
-
Lecture 20 (Thu, Mar 28):
Midterm exam
(on the material covered in Lectures 1-18).
-
Lecture 21 (Tue, Apr 2):
Saddle-node, transcritical, and pitchfork bifurcations in
R2 (cont.):
supercritical pitchfork bifurcation in two dimensions
in a more complicated example (Example 8.1.3)
[pages 246-248 of Sec. 8.1]
Hopf bifurcations:
proof that if λ is a root of a polynomial equation
with real coefficients, then its complex conjugate is also a root,
consequence: the roots of such equations are either real
or come in pairs of complex conjugate roots
[pages 248-249 of Sec. 8.2]
-
Lecture 22 (Thu, Apr 4):
Hopf bifurcations (cont.):
supercritical Hopf bifurcation: model system,
linearization around the fixed point,
behavior of the amplitude and the frequency
for a generic supercritical Hopf bifurcation:
amplitude = O((μ-μc)1/2),
frequency = O(1);
subcritical Hopf bifurcation: model system,
amplitude and the frequency near the bifurcation point
[Sec. 8.2]
Oscillating chemical reactions:
Belousov-Zhabotinskii (BZ) reaction - a brief discussion
of its history, theory, and importance;
watch a movie showing the
BZ reaction
(watch from the 7th minute on),
and a movie of
spatial patterns
due the BZ reaction
[Sec. 8.3]
Global bifurcation of cycles:
saddle-node bifurcation of cycles:
model system, amplitude and frequency are both O(1)
[pages 260-262 of Sec. 8.4]
-
Lecture 23 (Tue, Apr 9):
Global bifurcation of cycles (cont.):
infinite-period bifurcation, homoclinic bifurcation
[pages 262-265 of Sec. 8.4; skip Example 8.4.1]
Coupled oscillators and quasiperiodicity:
the plane R2,
the cylinder S1×R1,
and the torus T2;
functions defined on the torus
f:T2→R
(i.e., functions of two arguments that are periodic in each argument);
the solutions of the system
dθ/dt=ω where
θ=(θ1,θ2):R→T2
is a function with values in T2
and ω=(ω1,ω2)
is a constant vector are straight lines in the direction of
ω;
a necessary and sufficient condition for a straight line "wrapped" on
T2 to be closed:
ω1/ω2=p/q∈Q
(where Q is the set of rational numbers)
- a proof of this fact by representing a line on
T2 as a line on R2 with
the appropriate identifications;
analysis of the case ω=(3,2): the solution of
dθ/dt=ω in this case is a trefoil
knot!
[pages 275-276 of Sec. 8.6]
-
Lecture 24 (Thu, Apr 11):
Coupled oscillators and quasiperiodicity (cont.):
the solutions of the system
dθ/dt=ω where
ω=(ω1,ω2)
is a constant vector with
ω1/ω2∉Q
(where Q is the set of rational numbers)
is a straight line in the direction of ω
that fills the torus T2 densely
- quasiperiodic flow;
reduction of the coupled system
dθ1/dt=ω1+K1sin(θ2−θ1),
dθ2/dt=ω2+K2sin(θ1−θ2)
to a one-dimensional system
dφ/dt=ω1−ω2−(K1+K2)sinφ
for the difference
φ:=θ1−θ2:R→S1
of the angles θ1 and θ2,
saddle-node bifurcation of the equation for φ at
|ω1−ω2|=K1+K2,
fixed points for the equation for φ - phase-locked
(frequencey-locked, mode-locked) regime, compromise
frequency
[Sec. 8.6]
Poincare maps:
surface of section Σ
for an autonomous system
dx/dt=f(x)
of ODEs in ODEs in Rn
- an (n−1)-dimensional surface
in Rn transversal to
the vector field f,
definition of the Poincare map
P:Σ→Σ,
corespondence [periodic trajectory of
dx/dt=f(x)] ↔
[fixed point of the Poincare map]
(or more generally, a periodic point of the Poincare map),
stability of a fixed point of the Poincare map P
and its relation with the stability of the corresponding
periodic trajectory of dx/dt=f(x)
[pages 278-279 of Sec. 8.7]
-
Lecture 25 (Tue, Apr 16):
Poincare maps (cont.):
a cobweb construction of the orbit of a one-dimensional map,
more examples;
linear stability of periodic orbits,
characteristic multipliers (Floquet multipliers) of a periodic orbit
- the eigenvalues of the linearized Poincare map
at the corresponding fixed point
[pages 279, 281, 282 of Sec. 8.7]
Lorenz equations:
chaotic whaterwheel - a brief description and a
video,
Lorenz equations.
-
Lecture 26 (Thu, Apr 18):
A digression:
on the goals and methods of theory of dynamical systems.
Simple properties of Lorenz equations:
nonlinearity and symmetry properties of the Lorenz equations;
volume contraction and consequences (nonexistence of quasiperiodic
solutions, impossibility of repelling fixed points and repelling
periodic orbits), fixed points
[pages 311-314 of Sec. 9.2]
-
Lecture 27 (Tue, Apr 23):
Simple properties of Lorenz equations (cont.):
linear stability of the origin
0=(0,0,0), proving the global stability of the origin
for r<1 by using a Lyapunov function;
linear stability of the fixed points C+
and C− for 1<r<rH,
a saddle cycle around each of C±
- an unstable limit cycle
with a two-dimensional unstable manifold and a two-dimensional
stable manifold, a subcritical Hopf bifurcation at
rH - the stable fixed point C+
coalesce with the stable limit cicle around it into an unstable
fixed point (and similarly for C−)
[pages 314-319 of Sec. 9.2]
Chaos on a strange attractor:
numerical integration results in Lorenz's paper (1963);
exponential divergence of nearby trajectories,
measuring the exponential divergence "experimentally",
Lyapunov exponents, the exponential divergence is dictated
by the largest Lyapunov exponent,
consequences for numerical studies of systems
exhibiting exponential growth of the disturbances
[pages 317-323 of Sec. 9.3]
-
Lecture 28 (Thu, Apr 25):
Chaos on a strange attractor (cont.):
a working definition of chaos,
definition of attractor, example,
strange attractor
[pages 323-325 of Sec. 9.3]
Lorenz map:
defining a map that gives the (n+1)st
maximum of the z coordinate
as a function of the nth maximum of the z coordinate:
zn+1=f(zn),
stability and instability of fixed points and periodic orbits
of maps, ruling out stable limit cycles of the Lorenz system
by considering the Lorenz map
[Sec. 9.4]
Exploring parameter space:
brief remarks about the behavior of the solutions
of the Lorenz system for different parameter values
[pages 330-332 of Sec. 9.5]
-
Lecture 29 (Tue, Apr 30):
Complicated behavior of simple maps:
discussion of the paper
R.M.May, Simple mathematical models with very complicated dynamics,
Nature 261 (1976), 459-476;
Feigenbaum's universality.
-
Lecture 30 (Thu, May 2):
Turbulence and chaos:
a brief introdution of different approaches towards
studies of turbulence;
a discussion of the paper
J.-P.Eckmann, Roads to turbulence in dissipative dynamical
systems, Reviews of Modern Physics 53 (1981), 643-654.
Attendance:
You are required to attend class on those days when an
examination is being given;
attendance during other class periods is also expected.
You are fully responsible for the
material covered in each class, whether or not you attend.
Make-ups for missed exams will be given only if
there is a compelling reason for the absence,
which I know about beforehand
and can document independently of your testimony
(for example, via a note or a phone call from a
doctor or a parent).
Homework:
Homework will be assigned regularly and will be posted on the this
web-site.
The homework will be due at the start of class on the due date.
Each homework will consist of several problems,
of which some pseudo-randomly chosen problems will be graded.
THe lowest homework grade will be dropped.
Giving just an answer to a problem is not worthy any credit
- you have to write a complete solution which gives your
step-by-step reasoning and is written in grammatically correct English.
Although good exposition takes time and effort, writing your thoughts carefully
will greatly increase your understanding and retention of the material.
You are allowed to discuss the homework problems with the other students in the class.
However, each of you will need to prepare individual solutions
written in your own words - this is the only way to
achieve real understanding!
Your homework should have your name clearly written on it, and should
be stapled. Please write the problems in the same order in which they
are given in the assignment.
No late homework will be accepted!
Exams:
There will be one in-class midterm and a (comprehensive) final.
A tentative date for the midterm is
March 12 (Tuesday).
The final will be given from 1:30 to 3:30 p.m. on May 7 (Tuesday).
All tests must be taken at the scheduled times,
except in extraordinary circumstances.
Please do not arrange travel plans that prevent you
from taking any of the exams at the scheduled time.
Grading:
Your grade will be determined by your performance
on the following coursework:
| Coursework |
Weight |
| Homework (lowest grade
dropped) |
45% |
| Midterm exam |
20% |
| Final exam |
35% |
Technology:
We will frequently engage in computations to illustrate
the mathematical results that we discuss.
You will have to do some elementary programming in Mathematica
and MATLAB which are avaliable on the computers in the University's
computer labs, in particular, in the College of Arts and Sciences
computer labs in the Physical Sciences Center (room 232).
The amount of programming you will need to do will be small,
and previous programming experience is not assumed.
Useful links:
the
academic calendar,
the
class schedules.
Policy on W/I Grades :
From January 29 (Tuesday) to March 29 (Friday), you can withdraw
from the course with an automatic "W".
Dropping after April 1 (Monday) requires a petition to the Dean.
(Such petitions are not often granted.
Furthermore, even if the petition
is granted, I will give you a grade
of "Withdrawn Failing" if you are
indeed failing at the time of your petition.)
Please check the dates in the
academic calendar!
The grade of "I" (Incomplete)
is not intended to serve as
a benign substitute for the grade of "F".
I only give the "I" grade
if a student has completed the majority
of the work in the course
(for example everything except the final exam),
the coursework cannot be completed
because of compelling and verifiable problems
beyond the student's control, and the student expresses a clear
intention of making up the missed work as soon as possible.
Academic Misconduct: All cases of suspected academic
misconduct will
be referred to the Dean of the College of Arts and Sciences for
prosecution
under the University's Academic Misconduct Code. The penalties can be
quite
severe. Don't do it!
For details on the University's
policies concerning academic integrity see the
Student's Guide to Academic Integrity
at the
Academic Integrity web-site.
For information on your rights to appeal charges
of academic misconduct consult the
Academic Misconduct Code.
Students are also bound by the provisions of the
OU Student
Code.
Students With Disabilities:
The University of Oklahoma is committed to providing reasonable
accommodation
for all students with disabilities. Students with disabilities who
require
accommodations in this course are requested to speak with the
instructor
as early in the semester as possible. Students with disabilities must
be
registered with the Office of Disability Services prior to receiving
accommodations in this course. The Office of Disability Services is
located
in Goddard Health Center, Suite 166: phone 405-325-3852 or TDD only
405-325-4173.
MATLAB tutorials:
Good to know: