MATH 4513 - Senior Mathematics Seminar, Sec. 001 - Fall 2015
MWF 12:30-1:20 in 120 PHSC
Instructor: Prof. Nikola Petrov, 802 PHSC, (405)325-4316, npetrov AT math.ou.edu
Office Hours:
M 2:30-3:30, W 11:20-12:20, or by appointment, in 802 PHSC
First day handout
Check out the
OU Math Blog!
It is REALLY interesting!
A link
to the schedule of the presentations
The final projects in pdf format must be e-mailed to me
no later than 12 noon on Friday, Dec 18.
Homework:
-
Homework 1,
due on September 4 (Friday) (at the beginning of class).
-
Homework 2,
due on September 11 (Friday) (at the beginning of class).
-
Homework 3,
due on September 21 (Monday) (at the beginning of class).
-
Homework 4,
due on October 7 (Wednesday) (at the beginning of class).
-
Homework 5,
due on October 21 (Wednesday) (at the beginning of class).
Content of the lectures:
-
Lecture 1 (Mon, Aug 24):
Basic idea of theory of dynamical systems:
analyze the behavior of the solutions of an ordinary differential equation
(ODE) or a map without finding the solutions explicitly.
Existence and uniqueness of solutions of an initial value problem (IVP) for an ODE:
autonomous vs. non-autonomous ODEs;
example of an ODE without a solution:
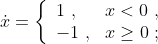
example of an ODE with infinitely many solutions
(formation and growth of a droplet in an oversaturated vapor),
physical reasons for the nonuniqueness of the solution of the mathematical problem.
-
Lecture 2 (Wed, Aug 26):
Flows on the line - a geometric way of thinking:
flow φt(x0)of an IVP
- the solution x(t) of the IVP
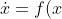, \ x(0)=x_0) ;
analyzing the asymptotic behavior of the solutions of IVP
;
analyzing the asymptotic behavior of the solutions of IVP
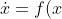, \ x(0)=x_0) by analysis of the graph of the right-hand side ƒ(x) of the ODE as a function of x;
phase plane - the plane with coordinates
by analysis of the graph of the right-hand side ƒ(x) of the ODE as a function of x;
phase plane - the plane with coordinates
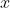 and
and
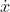 - the graph of the right-hand side ƒ(x) of the ODE is a line in this plane (why?);
finding its fixed points (FPs)
- the graph of the right-hand side ƒ(x) of the ODE is a line in this plane (why?);
finding its fixed points (FPs)
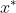 (satisfying
(satisfying
=0) );
classification of the FPs: stable FPs (atracting FPs, attractors, sinks),
unstable FPs (repelling FPs, repellers, sources),
semi-stable FPs (attracting on one side, repelling on the other side),
neutral (indifferent) FPs (neither attracting, nor repelling);
recognizing the type of a fixed point from the graph of ƒ(x) nearby.
);
classification of the FPs: stable FPs (atracting FPs, attractors, sinks),
unstable FPs (repelling FPs, repellers, sources),
semi-stable FPs (attracting on one side, repelling on the other side),
neutral (indifferent) FPs (neither attracting, nor repelling);
recognizing the type of a fixed point from the graph of ƒ(x) nearby.
-
Lecture 3 (Fri, Aug 29):
Linearization of an ODE near a fixed point:
studying the time evolution of the solution x(t)=x*+η(t)
of the IVP
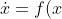, \ x(0)=x^* + \eta_0) ,
where |η0| is small, so that η02 can be neglected
in comparison with η0;
deriving of the variational equation
,
where |η0| is small, so that η02 can be neglected
in comparison with η0;
deriving of the variational equation
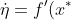\eta(t) + (1/2) f''(x^*)\eta(t)^2+\cdots, \ \eta(0)=\eta_0) of the ODE
of the ODE 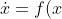) ;
solving the variational equation when
;
solving the variational equation when
\neq 0) ,
so that the terms with the higher powers of η(t) can be neglected and the IVP becomes
,
so that the terms with the higher powers of η(t) can be neglected and the IVP becomes
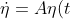, \ \eta(0)=\eta_0) with
with
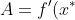) :
the solution is
:
the solution is
=\eta_0 e^{At}) ,
so that when
,
so that when 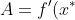>0) the η(t) grows exponentially so that the solution x(t) is unstable,
and when
the η(t) grows exponentially so that the solution x(t) is unstable,
and when 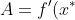<0) goes exponentially to 0 so that the solution x(t) is stable.
goes exponentially to 0 so that the solution x(t) is stable.
-
Lecture 4 (Mon, Aug 31):
Modeling of population dynamics:
naive approach to modeling a population P(t) -
the rate of change dP/dt is proportional
to the population P at the given moment:
dP/dt=αP(t)
with reproduction rate α=const>0 (taking into account
the birth and the death of individuals);
a problem with this model - the population
P(t)=P0eαt
grows unboundedly with t;
a modification of the model accounting for the limited resources
by introducing a term keeping P(t) bounded
- dP/dt=αP(1−P/K),
where K=const>0 is the carrying capacity of the system;
change of variables from P and dt to the non-dimensional variables
y:=P/K, τ:=αt,
to obtain the logistic equation,
dy/dτ=y(1−y);
taking into account constant harvesting
(i.e., removing a fixed number of individuals every time interval):
dP/dt=αP(1−P/K)−H,
non-dimensionalizing:
dy/dτ=y(1−y)−h,
where h:=H/(αK)=const>0
[see Deconinck's notes, Sec. 3.6 (pages 13-16)]
-
Lecture 5 (Wed, Sep 2):
Saddle-node bifurcation:
the simplest ODE exhibiting a saddle-node bifurcation:
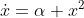 ;
a more complicated example:
;
a more complicated example:
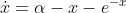 studied by expanding the right-hand side in a Taylor series around
(x*=0,α=1)
[see Deconinck's notes, Sec. 4.1 (pages 27-32)]
studied by expanding the right-hand side in a Taylor series around
(x*=0,α=1)
[see Deconinck's notes, Sec. 4.1 (pages 27-32)]
-
Lecture 6 (Fri, Sep 4):
Transcritical bifurcation:
derivation and examples of transcritical bifurcation -
exchange of stability of the fixed points
[see Deconinck's notes, Sec. 4.2 (pages 32-33)]
A digression:
slide rule
- based on the formula
ln(xy)=ln x ln y.
-
Lecture 7 (Wed, Sep 9):
Pitchfork bifurcation:
derivation and examples of transcritical bifurcation
[see Deconinck's notes, Sec. 4.3 (pages 33-35)]
Insect outbreak:
setting up the equation governing the population of spruce budworms
taking into account the limited resources and predation by
(a constant population of) birds
[see Deconinck's notes, Sec. 4.5 (pages 36-39)]
-
Lecture 8 (Fri, Sep 11):
Insect outbreak (cont.):
analysis of the bifurcations in the model of population of spruce budworms
- bistability, bifurcation diagram, hysteresis
[see Deconinck's notes, Sec. 4.5 (pages 39-44)]
-
Lecture 9 (Mon, Sep 14):
Two-dimensional linear systems:
general properties of linear systems;
an example: harmonic oscillator with and without air resistance
(using Newton Secold Law and Hooke's Law),
converting one higher-order ODE into a first-order system,
representation of the solution of the harmonic oscillator
in the phase plane (i.e., the (x1,x2)-plane);
a motivating example: studying the behavior of the solutions
of the linear system
dx1/dt=ax1,
dx2/dt=x2,
in the cases a>1 (unstable node), a=1 (unstable star),
0<a<1 (unstable node),
a=0 (a line of fixed points)
[see Deconinck's notes, Sec. 6.1, 6.2 (pages 51-56)]
-
Lecture 10 (Wed, Sep 16):
Two-dimensional linear systems (cont.):
a motivating example: studying the behavior of the solutions
of the linear system
dx1/dt=ax1,
dx2/dt=x2,
in the case a<0 (saddle point, stable and unstable manifolds).
Stability of fixed points of two-dimensional linear systems:
Lyapunov stable FP; attractive FP; asymptotically stable FP; examples
[see Deconinck's notes, Sec. 6.3, 6.4 (pages 57-60)]
-
Lecture 11 (Fri, Sep 18):
Linear algebra for linear systems:
eigenvectors and eigenvalues of a linear system;
solving a linear system by using the eigenvectors of the coefficient matrix;
imposing initial conditions to find the arbitrary constants,
geometric meaning of the condition for solvability of the linear system
for the arbitrary constants
[see Hirsch-Smale-Devaney, Sec. 2.3-2.6 (pages 26-36)]
-
Lecture 12 (Mon, Sep 21):
Phase portraits for planar linear systems:
phase portrait of an n-dimensional linear system
if all eigenvalues are real and distinct;
an example of a 2-dimensional linear system with two distinct eigenvalues;
an example of a 2-dimensional linear system
if the two eigenvalues are equal and their geometric multiplicity
(the dimension of the span of the eivenvectors corresponding
to this eigenvalue) is strictly smaller than their algebraic multiplicity
(their mulplicity as roots of the characteristic equation)
- obtaining the solution by solving the two equations consecutively
(to solve a linear non-homogeneous equation, use integrating factor μ(t));
exponential of a matrix; computing eA in practice
- first simplify (diagonalize if possible) the matrix A by a similarity transformation
A=CDC−1,
so that
Ak=CDkC−1,
and
eA=CeDC−1
[see Hirsch-Smale-Devaney, Sec. 3.1, 3.3 (pages 39-44, 47-49)]
Reading assignment (mandatory):
phase portrait of an 2-dimensional linear system
with complex eigenvalues - the case of a center (Re λ=0),
spiral sink (Re λ<0), and spiral source (Re λ>0)
[see Hirsch-Smale-Devaney, Sec. 3.2 (pages 44-47)]
-
Lecture 13 (Wed, Sep 23):
Phase portraits for planar linear systems (cont.):
writing the solution of the initial value problem
x'=Ax, x(0)=x(0) as
x(t)=eAtx(0);
changing coordinates in the case of distinct real eigenvalues
[see Hirsch-Smale-Devaney, Sec. 3.2 (pages 49-53)]
Why studying linear systems is important:
the existence and uniqueness of solutions of first-order systems
guarantees that the integral lines in the phase plane do not intersect;
the fixed points and the invariant manifolds "organize" the global dynamics.
-
Lecture 14 (Fri, Sep 25):
The trace-determinant plane:
writing the characteristic equation in the form
λ2−tr(A)λ+det(A)=0;
invariance of tr(A) and det(A) under change of variables
(i.e., under replacing A by CAC−1);
trace-determinant plane
[see Hirsch-Smale-Devaney, pages 61-64 of Sec. 4.1]
-
Lecture 15 (Mon, Sep 28):
Linearization around a fixed point:
linearizing a nonlinear equation
x'(t)=f(x)
around a fixed point x*
(satisfying f(x*)=0):
set
x(t)=x*+u(t)
so that |u(t)| is small;
the small displacement u(t)
satisfies a constant-coefficient linear system
u'(t)=Ax,
where A=Df(x*) is the consant matrix with entries
Aij=(∂fi/∂xj)|x*.
-
Lecture 16 (Wed, Sep 30):
Linearization around a fixed point (cont.):
simple examples of linearization;
prediction of the behavior of the linearized system
based only on looking at the eigenvalues;
"bad" cases - when the real part of an eigenvalue is 0.
-
Lecture 17 (Fri, Oct 2):
Linearization around a fixed point (cont.):
a detailed study of the solutions of the system
x'=x+y2,
y'=−y
and its linearization
u'=Df(x*)u
at the fixed point x*=0,
stable and unstable manifolds of the original system;
Mathematica plots of the integral lines of the linearized
and the original system in a
small domain
containing the fixed point x*=0
and in a
large domain
containing the fixed point
[see Hirsch-Smale-Devaney, Sec. 8.1 (pages 159-162)]
-
Lecture 18 (Mon, Oct 5):
Linearization around a fixed point (cont.):
transforming the system
x'=x+y2,
y'=−y
into its linearization at 0,
X'=X, Y'=−Y
by the change of variables
X=x+y2/3,
Y=y;
discussion of the stable and unstable manifolds
[see Hirsch-Smale-Devaney, Sec. 8.1 (pages 159-162)]
-
Lecture 19 (Wed, Oct 7):
Linearization around a fixed point (cont.):
a detailed solution of the harmonic oscillator written as a 2-dimensional system
- attracting spirals (in the presence of a resistance term),
centers (in the absence of a resistance term),
repelling spirals (in the presence of a "resistance" term with the "wrong sign"),
ability to change the behavior of the solutions of the resistance-free
harmonic oscillator by adding an arbitrarily small "resistance" term
(with the "right" or with the "wrong" sign);
an example of situation when the behavior of the solutions of the linearized
system is dramatically different from the behavior of the solutions
of the original system around the fixed point (Examples on page 164, 165);
Hartman-Grobman Theorem: when the fixed point is hyperbolic, there exists
a change of variables ("conjugacy") that changes the solutions of the linearized system
to the solutions of the original system
[see Hirsch-Smale-Devaney, Sec. 8.1 (pages 164, 165)]
-
Lecture 20 (Mon, Oct 12):
Bifurcations:
a reminder: saddle-node bifurcation in one dimension;
saddle-node bifurcation in a 2-dimensional system (Example on page 178-179)
[see Hirsch-Smale-Devaney, Sec. 8.5 (pages 175, 176, 178, 179)]
-
Lecture 21 (Wed, Oct 14):
Bifurcations (cont.):
Hopf bifurcation
[see Hirsch-Smale-Devaney, Sec. 8.5 (pages 181-182)]
Reading assignment (mandatory):
bifurcations in the system
r'=r−r3,
θ'=sin2θ+a
[see Hirsch-Smale-Devaney, Sec. 8.5 (pages 181-182)]
-
Lecture 22 (Fri, Oct 16):
A digression
on the two elevators in the Physical Sciences center,
the Intermediate Value Theorem, the Bisection Method
and the Newton Method for one-dimensional root finding,
and the pros and cons of these methods
(Bisection: always converges, root is bracketed, but the convergence is slow;
Newton: may not converge, root is not bracketed, but the convergence is extremely fast).
Nullclines:
an xi-nullcline of the nonlinear system
x'=f(x)
(i.e.,
xi'=ƒi(x1,x2,...,xn)
for i=1,2,...,n)
for the unknown function x=(x1,x2,...,xn):(−ε,ε)→Rn;
generally, a nullcline is an (n−1)-dimensional surface in Rn;
the intersection of all nullclines is the set of all fixed points of the system;
an example of using nullclines to analyze the qualitative behavior of the solutions
of a planar nonlinear system
[see Hirsch-Smale-Devaney, Sec. 9.1 (pages 187-190)]
-
Lecture 23 (Mon, Oct 19):
Nullclines:
heteroclinic and homoclinic bifurcations (examples of global bifurcations);
discovering a heteroclinic bifurcation by using nullclines;
remarks about using dynamical systems methods for space mission design
- links to
part 1 and
part 2
of the lectures "Space mission design and invariant manifolds"
of Martin Wen-Yu Lo (NASA)
[see Hirsch-Smale-Devaney, Sec. 9.1 (pages 190-192)]
-
Lecture 24 (Wed, Oct 21):
Stability of equilibria:
introduction: what can one learn about the stability of a fixed point x*
from the eigenvalues of the matrix Df(x*) of the linearized system
(recall the Hartman-Grobman Theorem)
-
Lecture 25 (Fri, Oct 23):
Stability of equilibria (cont.):
Lyapunov function; Theorem on Lyapunov Stability;
geometric idea behind the proof of the theorem
[see Hirsch-Smale-Devaney, pages 192-193 of Sec. 9.2]
-
Lecture 26 (Mon, Oct 26):
Stability of equilibria (cont.):
more on the geometry behind Lyapunov Stability Theorem;
example - nonlinear pendulum with air resistance
θ'=ν, ν'=−(g/l)sin(θ)−(b/m)ν,
suspected Lyapunov funciton = the total energy,
L(θ,ν)=(ml2/2)ν2−mglcos(θ)
[see Hirsch-Smale-Devaney, pages 194-195 of Sec. 9.2]
-
Lecture 27 (Wed, Oct 28):
Stability of equilibria (cont.):
using the conjectured Lyapunov function to prove the asymptotic stability
of the lowest point at rest
(i.e., (θ=0,ν=0))
for the nonlinear pendulum;
α- and ω-limit sets;
example of an ω-limit set that is not a point
- the attracting limit cycle of the system
r'=r(1−r), θ'=1
[see Hirsch-Smale-Devaney, pages 195, 196, 200 of Sec. 9.2,
pages 213, 214 of Sec. 10.1]
-
Lecture 28 (Fri, Oct 30):
class cancelled.
-
Lecture 29 (Mon, Nov 2):
Limit cycles:
definition of a limit cycle; examples
[see Strogatz, Sec. 7.0 and 7.1]
-
Lecture 30 (Wed, Nov 4):
Ruling out closed orbits:
proof of absence of limit cycles in gradient systems;
physical meaning of the potential function;
proving the absence of limit cycles by using Lyapunov functions (sketch only)
[see Strogatz, pages 199-201 of Sec. 7.2]
-
Lecture 31 (Fri, Nov 6):
Ruling out closed orbits (cont.):
review of the integral theorems of Calculus
- Fundamental Theorem of Calculus,
Stokes Theorem
(and Green's Theorem as its particular case),
Divergence Theorem (in R3
and in R2);
using the
Divergence Theorem in R2
to prove Dulac's Criterion for absence of closed orbits
[see Strogatz, pages 202-203 of Sec. 7.2]
-
Lecture 32 (Mon, Nov 9):
Poincaré-Bendixson Theorem:
Poincaré-Bendixson Theorem for proving the existence of a closed orbit;
an example
[see Strogatz, pages 203-205 of Sec. 7.3]
-
Lecture 33 (Wed, Nov 11):
Midterm exam
-
Lecture 34 (Fri, Nov 13):
A digression: more cocktail-party math - rearrangments of
conditionally convergent series, Riemann Rearrangement Theorem.
-
Lecture 35 (Mon, Nov 16):
Poincaré-Bendixson Theorem (cont.):
oscillations in Sel'kov model for glycolysis:
general setting, nullclines, fixed point
[see Strogatz, pages 205, 206 of Sec. 7.3]
-
Lecture 36 (Wed, Nov 18):
Poincaré-Bendixson Theorem (cont.):
oscillations in Sel'kov model for glycolysis:
construction of a trapping region,
Hopf bifurcation, a bifuration curve in the (a,b)-parameter space
[see Strogatz, pages 206-209 of Sec. 7.3]
-
Lecture 37 (Fri, Nov 20):
Maps:
maps - basic definitions; fixed points of maps and their stability;
using maps to model natural phenomena.
-
Lecture 38 (Mon, Nov 23):
Maps:
discussion of the paper R.M.May
"Simple mathematical models with very complicated dynamics,"
Nature 261 (1976), 459-476.
-
Lecture 39 (Mon, Nov 30):
Maps:
logistic map,
period doubling, Feigenbaum universality.
-
Lecture 40 (Wed, Dec 2):
Presentations:
-
Kayla Epperson:
Fisher's equation
-
Craig Cole, Jay Patel:
Oscillations in chemical reactions
-
Lecture 41 (Fri, Dec 4):
Presentations:
-
Crystal Nassir, Jacquelyn Porter:
Dynamics of the SIR epidemiological model
-
Lecture 42 (Mon, Dec 7):
Presentations:
-
Ashley Young, Austin Fox:
Hysteresis, subcritical Hopf bifurcation
-
Jesse Doan, Sunny Choi:
Insect outbreak, hysteresis, bistability
-
Lecture 43 (Wed, Dec 9):
Presentations:
-
Hunter Cole, Theodore Mayo Ma Mayo:
Forced nonlinear oscillators, jumps
-
Grace Younger, Maureen Wolf:
Stability of inverted pendulum
-
Lecture 44 (Fri, Dec 11):
Presentations:
-
Nikola Petrov:
Fractals around us
Two very good documntaries about nonlinear dynamics, chaos, and fractals:
Last remarks, words of wisdom, tears, etc.
Good to know: