Math Circle Schedule

Spring 2025

	Oct 19, 2025 Time: 12:30pm-2:00pm Location: University of Oklahoma, Physical Sciences Center, Room 1105 601 Elm Ave, Norman, OK 73019. Speaker: Allen Wu Title: How to Divide a Cake Fairly Abstract: Alice and Bob are sharing a cake and need to divide it into two parts. Each one will not be satisfied unless he/she gets his/her fair share. A possible solution is to invite a third person arbitrator to do the division and allocation. But what if one of them is not satisfied with the result? Is there some method of division that will guarantee both of them are happy, even without the interference of an arbitrator? This problem has existed since antiquity. One solution, for instance, was described in the first book of the bible. In this talk, we will explore solutions to this problem, as well as different generalizations of it. Pictures: $10-19-25, Pic 1$ $10-19-25, Pic 2$ $10-19-25, Pic 3$
	Nov 2, 2025 Time: 12:30pm-2:00pm Location: University of Oklahoma, Physical Sciences Center, Room 1105 601 Elm Ave, Norman, OK 73019. Speaker: Mahak Jauhri Title: TBD Abstract: TBD
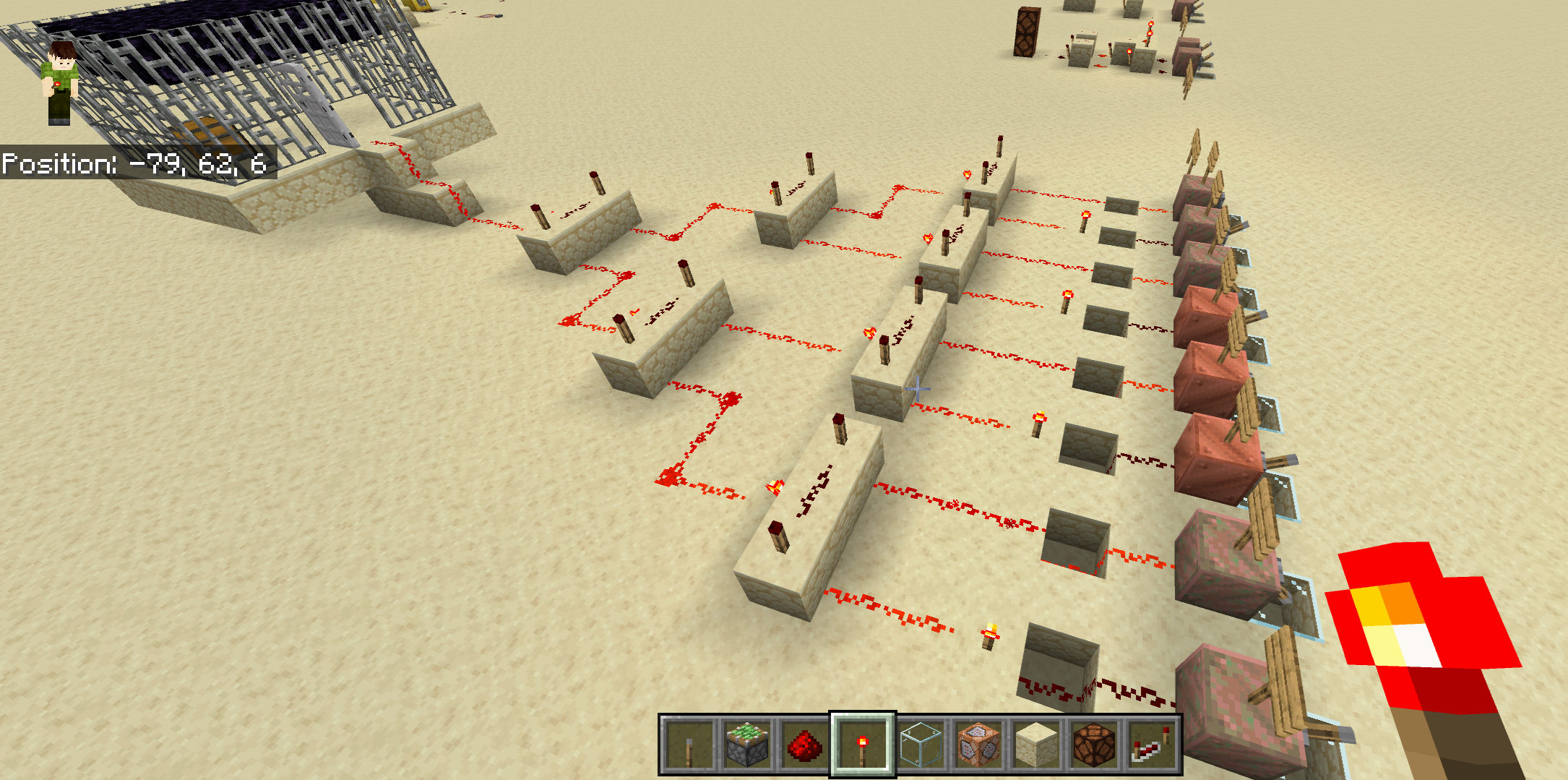
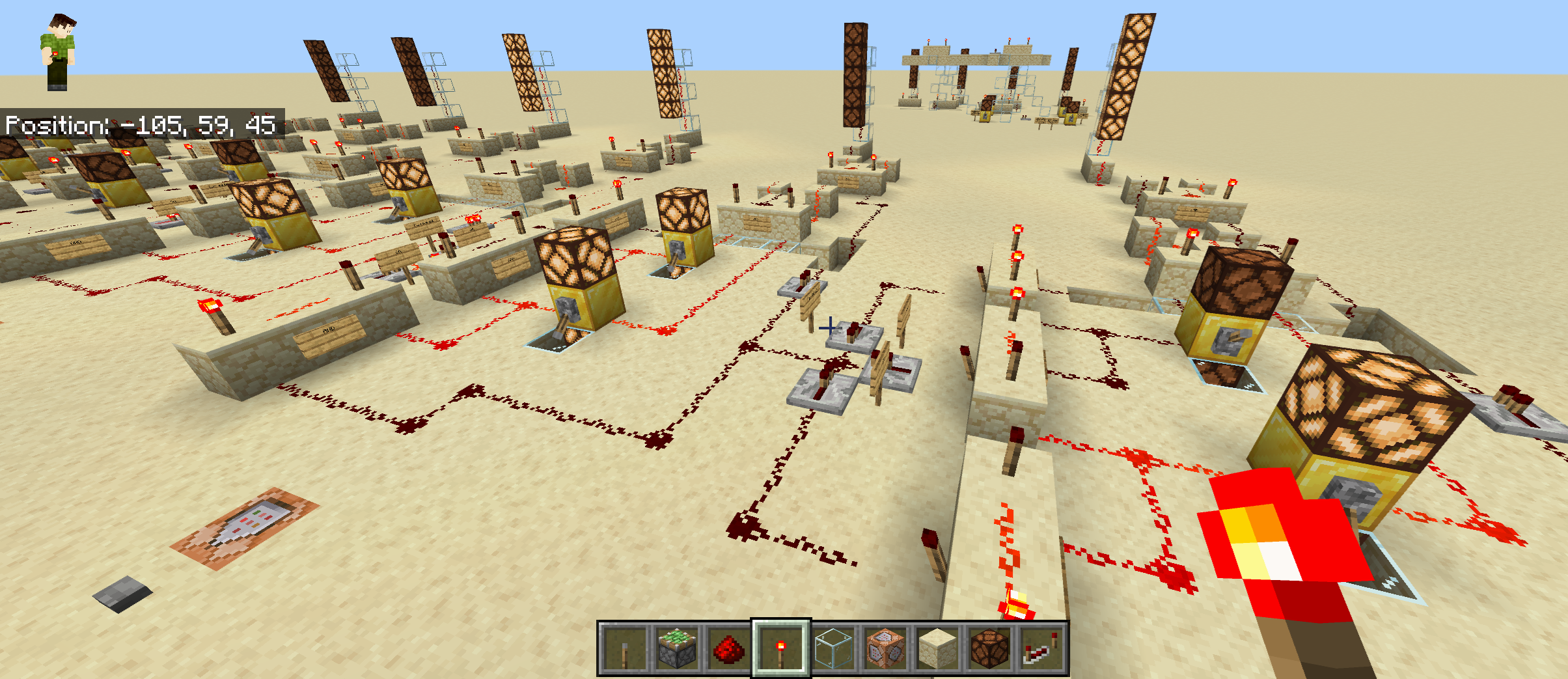
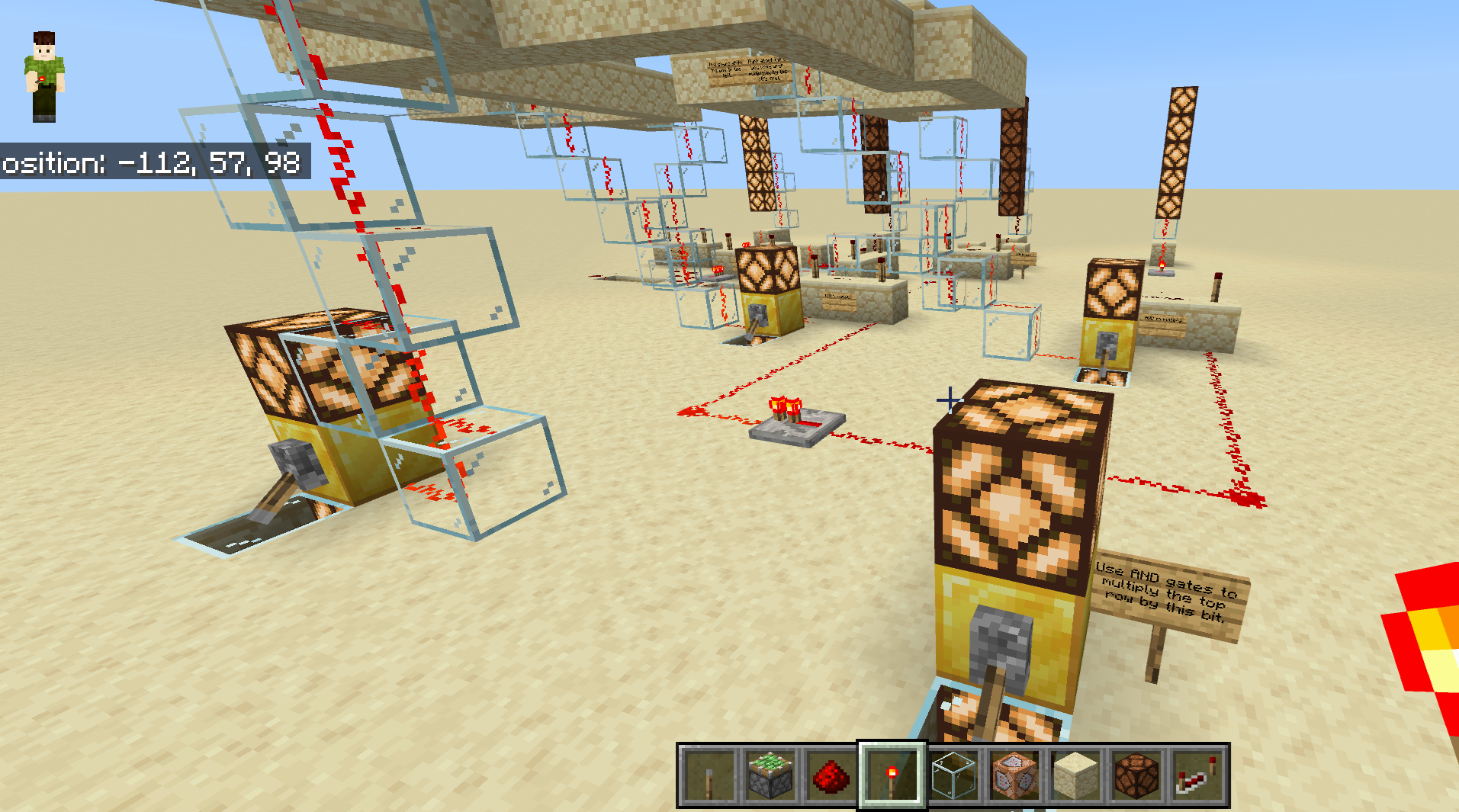
	Nov 9, 2025 Time: 12:30pm-2:00pm Location: University of Oklahoma, Physical Sciences Center, Room 1105 601 Elm Ave, Norman, OK 73019. Speaker: TBD Title: TBD Abstract: TBD
	Nov 16, 2025 Time: 12:30pm-2:00pm Location: University of Oklahoma, Physical Sciences Center, Room 1105 601 Elm Ave, Norman, OK 73019. Speaker: Elizabeth Kelley Title: TBD Abstract: TBD