MATH 4073 - Numerical Analysis, Section 001 - Fall 2016
MWF 10:30-11:20 p.m., 100 PHSC
Instructor:
Nikola Petrov, 802 PHSC, (405)325-4316, npetrov AT math.ou.edu.
Office Hours:
Tue 12:00-1:00 p.m., Fri 1:30-2:30 p.m., or by appointment, in 802 PHSC.
First day handout
Prerequisites:
MATH 3113 (Intro to ODEs) or 3413 (Physical Math I).
Course catalog description:
Solution of linear and nonlinear equations,
approximation of functions,
numerical integration and differentiation,
introduction to analysis of convergence and errors,
pitfalls in automatic computation,
one-step methods in the solutions of ordinary differential equations. (F)
Text:
R. L. Burden, J. D. Faires.
Numerical Analysis.
9th ed, Brooks/Cole, 2010, ISBN-10: 0538733519, ISBN-13: 978-0538733519.
The course will cover major portions of Chapters 1-5.
Homework
(after the due date solutions are deposited in Bizzell Library
and can be checked out from the Main Desk)
-
Homework 1, due Friday, Sep 2.
-
Homework 2, due Monday, Sep 12.
Codes needed for Homework 2:
-
Homework 3, due Wed, Sep 21.
-
Homework 4, due Fri, Sep 30.
-
Homework 5, due Fri, Oct 14.
A code needed for Homework 5:
- the MATLAB code
newton.m.
To use this code to find, say, a root of the equation
f(x)=x3−12=0,
you can type
newton( inline('x^3−12'), inline('3*x^2'), 3.0, 1e-14, 100, 1)
Here the first and the second arguments
are the function ƒ and its derivative;
the meaning of the other arguments is clear from the code
(see the
instructions
above how to run the code
bisection.m
that was needed for Homework 2).
Don't forget to type format long
in order to see more digits of the result.
Homework 6, due Mon, Oct 24.
Homework 7, due Wed, Nov 2.
Homework 8, due in class
on Mon, Nov 14.
Homework 9,
due Fri, Dec 2.
Codes needed for Homework 9:
- the MATLAB code
comp_trap.m;
-
instructions
how to run the MATLAB codes below for numerical solution of IVPs;
-
the MATLAB code
euler.m
from the book Numerical Methods Using MATLAB by J.H. Mathews and
K. D. Fink (4th edition, Pearson Prentice Hall, 2004),
and the MATLAB file rhs.m
for the example in the instructions above
(you have to write your own code rhs.m
for the problem in your homework).
Homework 10, due in class
on Fri, Dec 9.
Code needed for Homework 10:
Content of the lectures:
-
Lecture 1 (Mon, Aug 22):
Introduction:
on the importance of numerical analysis.
Review of calculus:
basic idea of calculus - split the object into "pieces" that are so "small"
that they can be treated approximately by using elementary methods;
an illustration - "deriving" a formula for the area of a circle
from the formula for the perimeter of the circle by slicing the circle
into a large number of identical sectors;
sequences and functions;
definition of a limit of a sequence: a number L
is a limit of a sequence an
(as n→∞) if for every ε>0
there exists a number K such that
an∈(L−ε,L+ε)
(or, equivalently, |an−L|<ε)
for every index n>K
[page 3 of Sec. 1.1]
Thinking assignments:
(1) think about the following sentence:
a sequence an can be considered as a function
a:N→R
(where N are the natural numbers, i.e., the set {1,2,3,...},
and R are the real numbers);
(2)
directly from the definition of limit of a sequence,
prove that the limit of the sequence an=1/n2
is 0 (hint: for any given ε>0 you may choose N=ε−1/2).
Reading assignment:
read and think about the definition of limit of a function (Definition 1.1),
and look at Figure 1.1
[page 2 of Sec. 1.1]
-
Lecture 2 (Wed, Aug 24):
Review of calculus (cont.):
continuous functions; Intermediate Value Theorem (IVT, Theorem 1.11);
using the IVT to prove the existence of a solution of an equation;
definition of a derivative of a function;
relationship between continuity and differentiability of a function;
Mean Value Theorem (MVT, Theorem 1.8); geometric meaning of the MVT;
using the MVT; Extreme Value Theorem (Theorem 1.9);
Riemann sums and integral
[pages 3-5, 8, 9 of Sec. 1.1]
-
Lecture 3 (Fri, Aug 26):
Review of calculus (cont.):
Mean Value Theorem for Integrals (a particular case of Theorem 1.13,
with g(x)≡1);
Fundamental Theorem of Calculus;
Taylor's Theorem (Theorem 1.14);
an example of application: computing
P3(x) and R3(x)
for the function sin(x) expanded about x0=0,
giving rigorous upper bounds on the error, |R3(x)|
[pages 10, 11 of Sec. 1.1]
Computer arithmetic:
binary, decimal and hexadecimal systems;
easy conversion between the hexadecimal and the binary system;
addition and multiplication in the binary system.
-
Lecture 4 (Mon, Aug 29):
Computer arithmetic (cont.):
bits and bytes; 1985 IEEE standard for a long real number;
sign, characteristic, and mantissa;
working with a finite number of digits - chopping and rounding;
roundoff errors - absolute and relative errors;
floating-point operations;
examples of roundoff errors - computing a sum;
solving a quadratic equation; nested way of computing polynomials
[Sec. 1.2]
-
Lecture 5 (Wed, Aug 31):
Computer arithmetic (cont.):
illustrating the loss of accuracy in MATLAB by executing the command
x=mod(2.0*x,1.0) multiple times in MATLAB,
starting with, say, x=pi;
testing the "machine epsilon" by comparing
(1+x) and 1 for smaller and smaller x,
NOT by comparing
x and 0 for smaller and smaller x
[see the Programming/thinking assignment below]
Algorithms and convergence:
pseudocode; loops;
counter-controlled ("for"),
condition-controlled ("while"),
conditional execution ("if", "then", "else");
example: computing the numerical value of the binomial
coefficient "n choose k" for large n;
rate of convergence of a sequence; "big O" notation; examples
[pages 32, 33, 37, 38 of Sec. 1.3]
Programming/thinking assignment:
Open MATLAB on your computer (or a computer in a computer lab),
download the MATLAB code
test_machine_epsilon.m,
(make sure that the downloaded file has the same name),
put this file in some directory that you will be using to save your codes,
type in the MATLAB command window the text
test_machine_epsilon(0) and press RETURN;
then type
test_machine_epsilon(1) and press RETURN again;
look at the code and at the output in the two cases;
in case you cannot run the code, here is the output
saved in the file output_test_machine_epsilon;
think about what the code does, and why were the results of the two runs were so different
(hint: it is related to the way numbers are stored in the memory of the computer).
-
Lecture 6 (Fri, Sep 2):
Algorithms and convergence (cont.):
stable, unstable and conditionally stable algorithms;
linear and exponential growth of the error
[page 34 of Sec. 1.3]
The bisection method:
general idea - based on the Intermediate Value Theorem;
algorithm; MATLAB code
bisection.m,
instructions how to run it,
and myfunction.m,
and the output
from running them;
the rate of convergence of the bisection method is O(2−n)
[pages 48-52, 54 of Sec. 2.1]
Fixed-point iteration:
fixed points,
relation between finding a zero and finding a fixed point;
graphical method of iterating a function;
fixed-point iteration;
iterating a function graphically
- a
cobweb diagram (cobweb plot, Verhulst diagram);
graphical examples of attracting and repelling fixed points
[pages 56, 57, 60 of Sec. 2.2]
Reading/thinking assignment:
stopping criteria [pages 49-50 of Sec. 2.1]
-
Lecture 7 (Wed, Sep 7):
Fixed-point iteration (cont.):
existence and uniqueness of fixed points: Theorem 2.3
- statement, intuitive graphical ideas behind its proof,
and proof of part (a);
an example of using Theorem 2.3: finding 21/2
as a root of the equation ƒ(x)=x2−1=0
or, equivalently, as a fixed point of the function
g(x)=x−ƒ(x)=x−x2+1;
more examples (Examples 2 and 3 on pages 58, 59);
Fixed Point Iteration (FPI) algorithm;
the MATLAB code
fixedpoint.m
[pages 57-61 of Sec. 2.2]
Reading assignments:
(1) Read the proof of part (b) of Theorem 2.4
[page 58 of Sec. 2.2]
(2) Read the statement of Theorem 2.4 (Fixed-Point Theorem)
and think how it is related to Theorem 2.3
[page 62 of Sec. 2.2]
(3) Read the Illustration on pages 61, 63, 64,
and think about the importance of reformulating an equation ƒ(x)=0
as a fixed-point problem g(p)=p
in an appropriate way.
-
Lecture 8 (Fri, Sep 9):
Newton's method:
idea: approximate the graph of the function near the root
by the tangent line to the graph;
derivation of the iterative formula;
numerical illustration in Mathematica of the fast convergence of the method
- the number of correct digits after the decimal point
approximately doubles at each step;
example: Newton's method for computing square roots;
problems with Newton's method:
(1) one needs a good choice of initial point p0,
otherwise the iteration may "get lost",
(2) one needs to compute the numerical value of the function's derivative at each step,
(3) the root is not necessarily bracketed;
secant method - does not involve computing derivatives
and instead of the tangent line to the graph at
(pn,ƒ(pn))
uses the straight line connecting the points
(pn−1,ƒ(pn−1))
and
(pn,ƒ(pn)),
reqiures two initial values,
p0 and p1,
to start the iteration
[pages 67-69, 71, 72 of Sec. 71]
-
Lecture 9 (Mon, Sep 12):
Lecture cancelled.
-
Lecture 10 (Wed, Sep 14):
Newton's method (cont.):
geometric interpretation of the secant method;
method of false position (Regula Falsi)
- the root is bracketed between pn
and pn-1 at each step
[pages 71, 73-75 of Sec. 2.3]
Error analysis of iterative methods:
order of convergence α
and asymptotic error constant λ
of a convergent sequence (and of an iterative method);
linear (α=1) and quadratic (α=2) convergence;
illustration of the speed of convergence
in the linearly and in the quadratically converging cases;
theorem about linear convergence of an iterative method
pn
= g(pn−1)
with g'(p)≠0
where p=g(p)=lim(pn)
as n→∞
- Theorem 2.8, with a "proof without words"
[pages 79, 80 of Sec. 2.4]
Reading assignment:
Read the proof of Theorem 2.8 [page 80 of Sec. 2.4]
-
Lecture 11 (Fri, Sep 16):
Error analysis of iterative methods (cont.):
theorem about quadratic convergence
of an iterative method
pn=g(pn−1)
with g'(p)=0
(Theorem 2.8, without proof);
constructing a quadratically convergent
iterative procedure from a zero-finding problem
(and obtaining the Newton's method as a result!);
multiplicity of a zero of a function; simple zeros;
example: the function ƒ(x)=cos(x)−1
has a zero of multiplicity 2 at p=0;
a C1 function ƒ has a simple zero at p
if and only if ƒ(p)=0 and ƒ'(p)≠0
(Theorem 2.11, with proof of the "if" part);
[pages 81-83 of Sec. 2.4]
Reading assignments:
(1)
Try to prove the "if" part of the proof of Theorem 2.11
without looking in the book;
hint: assume that ƒ(p)=0 and ƒ'(p)≠0,
expand ƒ in a zeroth Taylor polynomial about p:
ƒ(x)=ƒ(p)+ƒ'(ξ(x))(x−p),
use that ƒ(p)=0, take the limit x→p,
and use that ƒ∈C1, i.e., ƒ'∈C
[page 82-83 of Sec. 2.4]
(2)
Without looking in the book, use Theorem 2.11 to prove
the following generalization: The function ƒ∈C1[a,b]
has a zero of multiplicity m at p if and only if
0=ƒ(p)=ƒ'(p)=ƒ''(p)=...=ƒ(m−1)(p),
but ƒ(m)(p)≠0 (Theorem 2.12);
hint: the proof goes along the same lines as the proof of Theorem 2.11,
but in the "only if" part you have to consider ƒ(m(p)
instead of ƒ'(p),
and in the "if" part you have to use the (m−1)st Taylor polynomial,
i.e., to write
ƒ(x)=Tm−1(x)+Rm−1(x)
as in Taylor's Theorem (Theorem 1.14 on pages 10, 11 of the book).
-
Lecture 12 (Mon, Sep 19):
Error analysis of iterative methods (cont.):
relation between the multiplicity of a zero
and the number of vanishing derivatives
(Theorems 2.10, 2.11),
examples;
handling multiple zeros
- finding a simple zero of
μ(x)=ƒ(x)/ƒ'(x)
is equivalent ot finding a non-simple zero of ƒ(x)
[pages 83, 84 of Sec. 2.4]
Accelerating convergence:
derivation of the Aitken Δ2 method;
forward differences;
Aitken's method converges linearly, with error E*n
such that
lim(E*n/En)=0
where En is the original error
[pages 86-88 of Sec. 2.5]
-
Lecture 13 (Wed, Sep 21):
Accelerating convergence (cont.):
Steffensen's modification of a fixed-point iteration for accelerating convergence
(combination of fixed-point iteration and Aitken's method);
Steffensen's method converges quadratically!
[pages 88, 89 of Sec. 2.5]
Zeros of polynomials and Muller's method:
the Fundamental Theorem of Algebra (Theorem 2.16);
Corollary 2.17 (unique factorization of polynomials);
Corollary 2.18 (two polynomials of degree n
are identical if they have the same values at
n+1 distinct points);
Horner's method (synthetic division)
for computing values of polynomials at a given point
and for representing a polynomial P as
P(x)=(x−x0)Q(x)+b0
(with a proof)
[pages 91-93 of Sec. 2.6]
-
Lecture 14 (Fri, Sep 23):
Zeros of polynomials and Muller's method (cont.):
Horner's method (synthetic division) in practice;
method of deflation for finding zeros of polynomials;
computing P(pn−1)
and P'(pn−1)
in Newton's method for polynomials by using synthetic division;
if the non-real number z=a+bi (b≠0)
is a zero of multiplicity m of the polynomial P(x)
with real coefficients, then its complex conjugate
z*=a−bi is also a zero
of the same multiplicity of P(x),
and [(x−a)2+b2]m
is a factor of P(x)
(Theorem 2.10, with idea of proof);
Muller's method for finding complex zeros of polynomials
[pages 93-96 of Sec. 2.6]
-
Lecture 15 (Mon, Sep 26):
Zeros of polynomials and Muller's method (cont.):
Muller's method for finding complex zeros of polynomials
[pages 96-99 of Sec. 2.6]
Summary of zero-finding and fixed-point iteration:
-
Fixed point iteration: if {pn} is defined by
pn=g(pn−1)
and has a limit p, then:
-
if |g'(p)|∈(0,1), the sequence {pn}
converges linearly (with α=1) with asymptotic error constant
λ=|g'(p)|;
-
if |g'(p)|=0, the sequence {pn} converges with α>1.
-
Zero-finding methods:
-
bisection: α=1, λ=1/2, always converges;
-
Newton: α=2, sometimes doesn't converge;
-
secant: α=(51/2+1)/2=1.618... (the golden mean), sometimes doesn't converge;
-
Regula Falsi: always converges, usually (but not always) faster than bisection;
-
Muller: α=1.84... (the largest root of the equation
α3−α2−α−1=0), generally converges.
-
Mathematica notebooks
rate-of-convergence-blank.nb (blank version)
and rate-of-convergence-executed.nb
(version with all commands executed)
illustrating the different methods for zero-finding
on the example of the equation sin(x)+x=1,
treated with
(1) Newton's method,
(2) Secant method,
(3) fixed-point iteration
pn=g(pn−1)
with g(x)=1−sin(x)
(linear convergence with λ=|g'(0.5109734...)|=0.8722689...,
(4) fixed-point iteration with Aitken's extrapolation,
(5) Steffensen's method;
finally, it illustrates the trouble Newton's method has in finding the root
of the equation (sin(x)+x−1)3=0
because the root has multiplicity m=3.
-
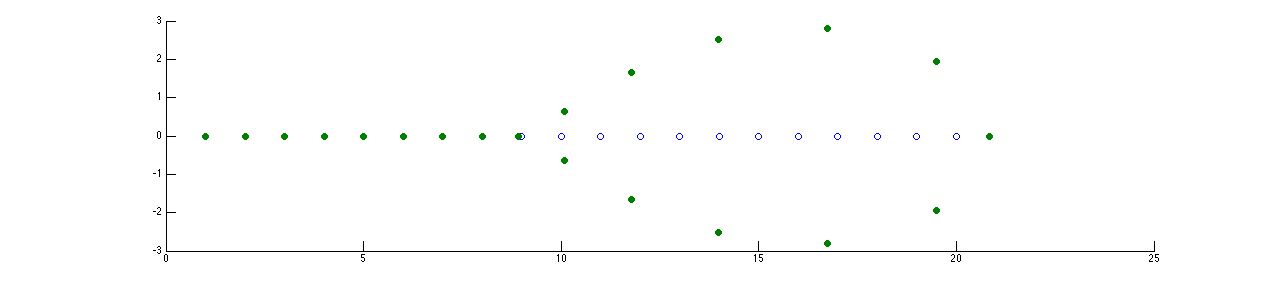
Sensitivity of numerical methods: Wilkinson's example: the roots of the polynomial
W(x)
= (x−1)(x−2)...(x−20)
= x20 − 210x19 + 20,615x18 − 1,256,850x17 + 53,327,946x16 − 1,672,280,820x15 + 40,171,771,630x14 − 756,111,184,500x13 + 11,310,276,995,381x12 − 135,585,182,899,530x11 + 1,307,535,010,540,395x10 − 10,142,299,865,511,450x9 + 63,030,812,099,294,896x8 − 311,333,643,161,390,640x7 + 1,206,647,803,780,373,360x6 − 3,599,979,517,947,607,200x5 + 8,037,811,822,645,051,776x4 − 12,870,931,245,150,988,800x3 + 13,803,759,753,640,704,000x2 − 8,752,948,036,761,600,000x1 + 2,432,902,008,176,640,000
are, clearly, the integers 1, 2, ..., 19, 20.
If the coefficient of x19 is changed from −210
to −210−2−23=−210.0000001192,
then the polynomial value W(20) decreases from 0 to
−2−232019=−6.25×1017,
and the roots of the modified polynomial are approximately
1.00000, 2.00000, 3.00000, 4.00000, 5.00000, 6.00001, 6.99970, 8.00727,
8.91725, 10.09527±0.64350i, 11.79363±1.65233i,
13.99236±2.51883i, 16.73074±0.81262i,
19.50244±1.94033i, 20.84691
- in the figure below, the original roots are represented by empty blue circles
and the new ones with full green circles.
Introduction to interpolation and approximation:
need of approximating data, idea of interpolation (Intro to Chapter 3).
Interpolation and Lagrange polynomial:
examples of polynomial interpolation with polynomials of degrees 0, 1, and 2;
idea of Lagrange interpolation: given data at
x0, x1, ..., xn,
construct a polynomial Ln,k(x) of degree n
that satisfies
Ln,k(xk)=1,
Ln,k(xj)=0
for j≠k
[pages 106-109 of Sec. 3.1]
-
Lecture 16 (Wed, Sep 28 ):
Interpolation and Lagrange polynomial (cont.):
expressing the Lagrange interpolating polynominal (LIP)
Pn(x)
as a linear combination of the polynomials
Ln,k(x)
with coefficients equal to the values ƒ(xk)
of the function ƒ that we approximate;
error bound in Lagrange interpolation (Theorem 3.3);
remark on the similarity between the expressions
for the error in Lagrange interpolation and
for the remainder approximating a function by its Taylor polynomial;
a sketch of an example of a local linear interpolation:
Example 4 - a piecewise-linear interpolation
for the function ƒ(x)=ex
on the interval [0,1]
[pages 110-112, 114 of Sec. 3.1]
Reading assignment:
Finish Example 4 on page 114.
-
Lecture 17 (Fri, 30)
Interpolation and Lagrange polynomial (cont.):
a brief discussion of Weierstrass Approximation Theorem (Theorem 3.1)
[page 106 of Sec. 3.1]
Divided differences:
idea - designing a way of writing the (unique) interpolating
polynomial Pn(x) of degree n
through (n+1) data points that is easier to use to compute
the value Pn(z)
of the interpolating polynomial for an arbitrary value z of the argument;
inspiration - the nested way of computing values of polynomials (recall Sec. 1.2);
notations for Newton's divided differences;
interpolating polynomial in Newton's divided differences form;
computing the divided differences manually (in a table);
efficiency of Newton's divided differences algorithm
- to compute the values of the coefficients
ak=ƒ[x0,xq,...,xk],
one performs O(n2) operations,
and to compute the value of Pn(z)
for an arbitrary z, one performs 2n operations
[pages 124-127 of Sec. 3.2]
-
Lecture 18 (Mon, Oct 3):
Exam 1,
on the material from Sections 1.1-1.3, 2.1-2.6,
covered in lectures 1-14.
-
Lecture 19 (Wed, Oct 5):
Divided differences (cont.):
a detailed derivation of the number of operations
that are needed to compute the values of the coefficients
ak=ƒ[x0,xq,...,xk]
for data consisting of n+1 points,
(x0,ƒ(x0)),
(x1,ƒ(x1)), ...,
(xn,ƒ(xn)):
-
the 0th order differences are equal to the function values,
ƒ[xk]=ƒ(xk),
so no computations are needed;
-
to compute the n 1st order differences
ƒ[xk,xk+1]
(k=0,1,...,n−1), one needs to perform 3n operations
(2n subtractions and ndivisions);
-
to compute the (n−1) 2nd order differences
ƒ[xk,xk+1,xk+2]
(k=0,1,...,n−2), one needs to perform 3(n−1) operations;
-
to compute the (n−2) 3rd order differences
ƒ[xk,xk+1,xk+2,xk+3]
(k=0,1,...,n−3), one needs to perform 3(n−2) operations;
-
...;
-
to compute the 2 (n−1)st order differences
ƒ[x0,x1,...,xn−1]
and
ƒ[x1,x2,...,xn]
one needs to perform 3×2 operations;
-
to compute the nth order difference
ƒ[x0,x1,...,xn],
one needs to perform 3×1 operations;
therefore the total number of operations is
3[n+(n−1)+(n−2)+...+2+1]=3n(n+1)/2=O(n2);
writing the formula for the Newton's divided differences polynomial
for equidistant set of points
x0,x1,...,xn,
i.e., xi=x0+ih
(i=0,1,2,...,n):
if
x=x0+sh
for some s∈[0,n],
then introduce the notation "s choose k" (s∈R, k∈{0,1,2,...})
and write
Pn(x)=Pn(x0+sh)
by using these notations
[page 129 of Sec. 3.3]
-
Lecture 20 (Mon, Oct 10):
Divided differences (cont.):
forward and backward differences;
forward-differences and backward-differences ways
of writing an interpolating polynomial;
note that in the formula using forward differences,
s∈[0,n] is defined by x=x0+sh,
while
in the formula using backward differences,
s∈[−n,0] is defined by x=xn+sh
[pages 129-131 of Sec. 3.3]
-
Lecture 21 (Wed, Oct 12):
Cubic spline interpolation:
on the origin of the word "spline";
general idea of spline interpolation; piecewise linear interpolation;
cubic spline interpolant S(x)
based on values of a function ƒ at n+1 nodes
x0<x1<x2<...<xn−1<xn
and its restrictions Sj(x)
to [xj,xj+1];
compatibility conditions on the functions Sj(x)
and their derivatives first and second derivatives at the internal nodes
xj+1 (j=0,1,...,n−2),
and compatibility of the values of the interpolant S(x)
with the function ƒ(x) at all nodes;
enumerating the conditions:
- compatibility of the values of the interpolant:
S0(x0)=ƒ(x0),
S0(x1)=ƒ(x1)=S1(x1),
S1(x2)=ƒ(x2)=S2(x2), ...,
Sn−2(xn−1)=ƒ(xn−1)=Sn−1(xn−1),
Sn−1(xn)=ƒ(xn)
- a total of 1+2(n−1)+1=2n conditions,
-
compatibility of the derivatives of the interpolant at the internal nodes:
S0'(x1)=S1'(x1),
S1'(x2)=S2'(x2),
S2'(x3)=S3'(x3), ...,
Sn−2'(xn−1)=Sn−1'(xn−1)
- a total of (n−1) conditions,
-
compatibility of the second derivatives of the interpolant at the internal nodes:
S0''(x1)=S1''(x1),
S1''(x2)=S2''(x2),
S2''(x3)=S3''(x3), ...,
Sn−2''(xn−1)=Sn−1''(xn−1)
- a total of (n−1) conditions,
-
two conditions coming from appropriately formulated requirements
on S0 at the left end node x0
and on Sn−1 at the right end node xn;
writing Sj(x) in the form
Sj(x)=aj+bj(x−xj)+cj(x−xj)2+dj(x−xj)3,
computing the first and second derivatives of Sj(x)
[pages 144-147 of Sec. 3.4]
-
Lecture 22 (Fri, Oct 14):
Cubic spline interpolation (cont.):
reformulating the conditions on
Sj(x)
in terms of the 4n coefficients aj, bj,
cj, dj:
-
the conditions that the functions Sj at all nodes
should have the same values as the function ƒ at all nodes
give us n+1 equations,
-
the conditions that two "adjacent" functions,
Sj and Sj+1
should have matching values, matching first derivatives,
and matching second derivatives where they meet
(i.e., at all internal nodes),
Sj(xj+1)=Sj+1(xj+1),
Sj'(xj+1)=Sj+1'(xj+1),
Sj''(xj+1)=Sj+1''(xj+1),
j=0,1,...,n−2,
give us 3(n−1) linear equations for the coefficients;
-
two more equations come from the boundary conditions imposed,
i.e., on conditions on the interpolant S(x)
at the boundary points x0 and xn:
either
-
free (natural) boundary conditions:
S''(x0)=0,
S''(xn)=0, or
-
clamped boundary conditions:
S'(x0) and S'(xn)
have known values, i.e., assuming that we know
ƒ'(x0) and ƒ'(xn),
we require that
S'(x0)=ƒ'(x0)
and
S'(xn)=ƒ'(xn);
after some elementary algebra, one can reduce the computation of the 4n
equations for the coefficients
to a system of linear equations that can be written as a matrix equation
A⋅c=v,
where A is a (n+1)×(n+1)
tridiagonal matrix, and the number of operations
to solve the system is O(n)
(while for a general (n+1)×(n+1)
matrix it is O(n3))
[pages 147-148 of Sec. 3.4]
-
Lecture 23 (Mon, Oct 17):
Cubic spline interpolation (cont.):
theoretical error bounds: error = O(h4) (Theorem 3.13);
remarks about the practical importance of cubic splines;
using splines in Matlab: the commands
interp1 and spline
perform spline interpolation and evaluation, illustrated by the following MATLAB commands
(>> is the line prompt, % comments out the rest of the line):
>> x = [0 20 40 56 68 80 84 96 104 110]; % values of x_i
>> f = [0 15 20 38 80 80 100 100 125 125]; % values of f(x_i)
>> t = linspace(0,110); % type 'help linspace' to read about this command
>> s = interp1(x,f,t,'spline'); % interpolating by using cubic splines
>> plot(x,f,'o',t,s) % plotting the date points (circles) and the interpolating spline (line)
these commands perform cubic spline interpolation of based on the data points
(x0,ƒ(x0))=(0,0),
(x1,ƒ(x1))=(20,15),
(x2,ƒ(x2))=(40,20),
(x3,ƒ(x3))=(56,38),
...,
(x10,ƒ(x10))=(110,125),
and evaluate the cubic spline interpolant at the 100 equidistant values
between 0 and 110 created by the command
linspace(0,110) (100 is the default value),
and plot all these on the same plot; try the same commands
by replacing the option 'spline'
in the command interp1(x,f,t,'spline');
by the options 'nearest' (nearest neighbor interpolation),
'linear' (piecewise linear interpolation),
or 'pchip' (piecewise cubic Hermite interpolation)
[page 160 of Sec. 3.5]
-
Lecture 24 (Wed, Oct 19):
Numerical differentiation:
basic idea - using Lagrange interpolating polynomials;
forward- and backward-difference two-point formulas (error = O(h));
idea of general (n+1)-point formulas for the first derivative;
derivation of general two-point formula for the first derivative
[pages 174-176 of Sec. 4.1]
-
Lecture 25 (Fri, Oct 21):
Numerical differentiation (cont.):
three-point formulas (error = O(h2));
formula for the second derivative derived from the Taylor expansion
(error = O(h2))
[pages 176, 177, 180 of Sec. 4.1]
Richardson extrapolation:
general idea
[pages 185, 186 of Sec. 4.2]
-
Lecture 26 (Mon, Oct 24):
derivation of expressions for N1(h),
N2(h), N3(h)
by using dividing h by 2 at each step;
idea for generalization to the case when
the difference M−N1(h)
has a general expansion in increasing powers of h
(as in equation (4.14))
[pages 186-188 of Sec. 4.2]
-
Lecture 27 (Wed, Oct 26):
Numerical integration:
goal; numerical quadrature; setup;
idea - using Lagrange interpolation polynomials;
weighted mean value theorem for integrals;
derivation of the quadrature formula and the expression
for the error for the trapezoidal method (using linear Lagrange interpolation)
- the error is O(h3);
sketch of derivation of the Simpson's formula for numerical quadrature
- instead of the "standard" way of deriving it by integrating the Lagrange
interpolating polynomial, use Taylor expansion of ƒ(x) about
x1, the error is O(h5)
[pages 193-197 of Sec. 4.3]
-
Lecture 28 (Fri, Oct 28):
Numerical integration (cont.):
degree of accuracy (precision) of a quadrature formula;
Newton-Cotes (N-C) formulas for numerical integration;
open and closed Newton-Cotes formulas;
examples of closed N-C formulas (trapezoidal, Simpson's,
Simpson's 3/8); idea of the open N-C formulas;
example of an open N-C formula - midpoint rule (error O(h3))
[page 197 of Sec. 4.3; brouse through pages 198-200 of Sec. 4.3]
Composite numerical integration:
derivation of the composite trapezoidal rule and the composite Simpson's rule;
sketch of the derivation of the error formulas of the composite trapezoidal and Simpson's rules
[pages 203-207 of Sec. 4.4]
Romberg integration:
idea - composite trapezoidal rule for different stepsizes h followed by Richardson's extrapolation
[page 213 of Sec. 4.5]
-
Lecture 29 (Mon, Oct 31):
Romberg integration:
discussion of the usefulness of Romberg integration.
Practical issues in numerical integration:
if the integrand becomes infinite at a point, use the Taylor expansion of the function
about that point to perform integration on a small interval around this point "by hand"
and use the computer to compute the value of the integral on the rest of the interval;
infinite limit(s) of integration - either choose a large enough interval [a,b]
such that the "tails" have small enough values (give upper bounds of the "tails"),
or change variables so that the limits of integration become finite
(useful functions that can do this are arctan and tanh).
-
Lecture 30 (Wed, Nov 2):
Gaussian quadrature:
idea and a simple example;
theoretical foundations of Gaussian quadrature:
linear space (vector space),
uniqueness of the zero element
[see the handout on Gaussian
quadrature]
Food for Thought:
prove the following properties:
(a) for every u∈V,
the opposite vector is unique (proof by contradiction);
(b) for every u∈V, 0u=0;
(c) the opposite vector of every u∈V
equals (−1)u;
(d) u+u=2u.
-
Lecture 31 (Fri, Nov 4):
Gaussian quadrature (cont.):
normed linear space;
examples of norms: l1-norm,
l2-norm, l∞-norm in Rn;
inner product linear space;
defining an inner product in Rn
by a symmetric positive-definite matrix;
Cauchy-Schwarz inequality;
linear space of polynomials of degree not exceeding n;
weight function w, inner product in a space of polynomials;
constructing an orthogonal family of polynomials
[see the handout on Gaussian
quadrature]
-
Lecture 32 (Mon, Nov 7):
Gaussian quadrature (cont.):
using orthogonal polynomials for numerical integration
- Lemma 1 and Theorem 1 in the
handout on Gaussian quadrature;
Legendre polynomials; an example
[Sec. 4.7]
-
Lecture 33 (Wed, Nov 9):
Elementary theory of IVPs for ODEs:
initial-value problems (IVPs) for ordinary differential equations
(ODEs) - definition, examples;
Lipschitz condition and Lipschitz constant;
examples of Lipschitz and non-Lipschitz functions;
relation of Lipschitz condition with continuity and with differentiability;
bounded derivative implies Lipschitz;
existence and uniqueness of solutions of an IVP for a first-order ODE;
well-posedness of an an IVP for a first-order ODE;
an example of an IVP without a solution;
an example of an IVP with infinitely many solutions -
equation of formation of a droplet of a liquid in saturated vapor
[Sec. 5.1]
-
Lecture 34 (Fri, Nov 11 ):
Elementary theory of initial-value problems (cont.):
formation of a droplet of a liquid in saturated vapor
- solving the equation in a "standard" way,
constructing infinitely many solutions,
physical explanation of the non-uniqueness,
mathematical reason (the function ƒ(V)=V2/3
is not Lipschitz on [0,a] for any a>0).
Euler's method:
geometric meaning of the equation
dy/dt=ƒ(t,y),
slope fields; constructing an approximate solution of an IFP
by hand by "following" the slope fields;
idea of Euler's method
[page 266 of Sec. 5.2]
-
Lecture 35 (Mon, Nov 14):
Euler's method (cont.):
deriving the Euler's method;
preparation for the error analysis of the Euler's method
(Lemmas 5.7 and 5.8);
statement of the theorem on the error of the Euler's method
(Theorem 5.9)
[pages 266-271 of Sec. 5.2]
-
Lecture 36 (Wed, Nov 16):
Exam 2,
on the material from Sections 3.1-3.5, 4.1-4.5, 4.7,
covered in lectures 15-17, 19-32;
see also the handout on Gaussian
quadrature.
-
Lecture 37 (Fri, Nov 18):
Euler's method (cont.):
proof of the theorem on the error of the Euler's method (Theorem 5.9);
finding empirically how the error depends on the stepsize h
[pages 271-272 of Sec. 5.2]
-
Lecture 38 (Mon, Nov 21):
Euler's method (cont):
error analysis of the Euler method - an example
[Sec. 5.2]
-
Lecture 39 (Mon, Nov 28):
Higher-order Taylor mehtods:
local truncation error,
proof that the local truncation error
of Euler's method is O(h);
derivation of higher-order Taylor methods; an example;
the error of the Taylor method of order n
is O(n) (Theorem 5.12, without proof),
practical difficulties of applying higher-order Taylor methods
[Sec. 5.3]
-
Lecture 40 (Wed, Nov 30):
Runge-Kutta methods:
Taylor Theorem in 2 variables (Theorem 5.13, without proof);
warm-up: derivation of the modified Euler method - a simple RK method
that has the same local truncation error
as the Taylor method of order 2
[pages 282, 283, 286 of Sec. 5.4]
-
Lecture 41 (Fri, Dec 2):
Runge-Kutta methods (cont.):
geometric interpretation of the modified Euler method
and comparison with Euler's method;
derivation of a more general RK2 method,
that approximates T(2)(t,w) by
bƒ(t,w)+cƒ(t+β,w+γ);
particular cases:
the modified Euler method (with b=1/2)
and the midpoint method (with b=0);
geometric interpretation of the midpoint method;
the classical RK method of order four
(without derivation)
[pages 284-286, 288 of Sec. 5.4]
-
Lecture 42 (Mon, Dec 5):
Error control and the Runge-Kutta-Fehlberg method:
using two methods of different accuracy
to control the error and adapt the stepsize h;
Runge-Kutta-Fehlberg method
[pages 293-297 of Sec. 5.5]
Free MATLAB tutorials online:
Good to know:
The greek_alphabet;
some useful notations.
