MATH 4433 - Introduction to Analysis I, Section 001 - Spring 2017
TR 10:30-11:45 a.m., 403 PHSC

Office Hours: Monday 2:30-3:30, Wednesday 10:30-11:30, or by appointment, in 802 PHSC.

First day handout

Course catalog description: Prerequisite: 2433 and 2513 or permission of instructor. Review of real number system. Sequences of real numbers. Topology of the real line. Continuity and differentiation of functions of a single variable. (F, Sp, Su)

Texts: All three books are feely available (in pdf format) for OU students from the OU library:
Stephen Abbott, Understanding Analysis, Springer, 2nd ed., 2015, ISBN: 978-1493927111.
Kenneth A. Ross, Elementary Analysis: The Theory of Calculus, Springer, 2nd ed., 2013, ISBN: 978-1461462705.
Asuman G. Aksoy, Mohamed A. Khamsi, A Problem Book in Real Analysis, Springer, 2010, ISBN: 978-1441912954.

Homework [read the following useful advice on writing proofs and advice from students]

• Homework 1, due January 26 (Thursday).
• Homework 2, due February 2 (Thursday).
• Homework 3, due February 9 (Thursday).
• Homework 4, due February 16 (Thursday).
• Homework 5, due March 2 (Thursday).
• Homework 6, due March 9 (Thursday).
• Homework 7, due March 23 (Thursday).
• Homework 7a, NOT due March 28 (Tuesday).
• Homework 8, due April 11 (Tuesday).
• Homework 9, due April 18 (Tuesday).
• Homework 10, due April 25 (Tuesday).
• Homework 10a, NOT due May 4 (Thursday).

Tentative course content:

• The real numbers: natural numbers, induction; real numbers, ordering, completeness, cardinality, Cantor's Theorem.
• Sequences and series: convergence, limit theorems, monotone sequences, subsequences, Bolzano-Weierstrass Theorem, Cauchy sequences; infinite series.
• Topology of R: the Cantor set, open and closed sets, compact sets.
• Limits and continuity: limits of functions, continuous functions, Intermediate Value Theorem, (uniform continuity).
• Differentiation: derivative, Mean Value Theorem, L'Hospital rule, Taylor's Theorem.
• Sequence and series of functions: sequences of functions, uniform convergence and differentiation; series of functions, power series, Taylor series.
• Integration: Riemann integral, Fundamental Theorem of Calculus.

Content of the lectures:

• Lecture 1 (Tue, Jan 17): Preliminaries: set notations: x∈A, x∉A, A⊆B, A=B, complement A^c of a set A, union A∪B and intersection A∩B of the sets A and B, relative complement A∖B:=A∩(B^c) of B in A, de Morgan's laws;
  B sets of natural numbers N, integers Z, rational numbers Q, real numbers R;
  logic notations: negation ∼S of a statement S, existential quantifier ∃, universal quantifier ∀, statement S implies statement R (S⇒R), statement S is equivalent to statement R (S⇔R), the contrapositive of S⇒R is defined as ∼R⇒∼S;
  proof by contradiction, example of a proof by contradiction: irrationality of the number 2^1/2.
  Reading: Aksoy, pages 1, 2; Abbott, pages 1, 2.
  FFT problems^*: Aksoy, problems 1.1, 1.8, 1.9 (on pages 4, 5, solved on pages 9-12).
  ^* FFT ("Food For Thought") problems are problems that you should be able to solve, but you do not have to turn in.
• Lecture 2 (Thu, Jan 19): Preliminaries (cont.): more examples of proofs related to sets; proving that A⊆B iff A∪B=B and that A⊆B iff A∩B=A (links to the solutions with blanks and the complete solutions); definition of a function, domain and range of a function; 1-to-1 (injective), onto (surjective), and bijective functions; examples (domains and ranges of the functions ƒ(x)=x², ƒ(x)=ln(x), ƒ(x)=[ln(x)]^1/2); a proof that g(A∪B)=g(A)∪g(B); proofs by induction.
  Reading: Abbott, pages 5-7, 10, 11; Aksoy, pages 2, 3.
  FFT problems: Aksoy, problems 1.2, 1.7, 1.8, 1.17, 2.3, 2.5 (on pages 4, 5, 7, 22, 23, solved on pages 9, 11, 14, 15, 27-29). Remark: in Problem 1.7, before trying to solve each part of the problem, draw the corresponding Venn diagram to make sure that the statement is reasonable.
  The complete Homework 1 is due on January 26 (Thursday).
• Lecture 3 (Tue, Jan 24): Preliminaries (cont.): Problem 1.8(a) on page 5, do part (b) yourselves, note that part (a) can be solved in at least two more methods (click here to see how);
  more about sets: proving that A∖B=(A^c)∖(A^c); useful set identities: A∪(B∩C)=(A∪B)∩(A∪C), A∩(B∪C)=(A∩B)∪(A∩C) (draw Venn diagrams); set notations in R, example: (0,3]^c=(−∞,0]∪(3,∞);
  on the example ƒ:A→B with A=R, B=R given by ƒ(x)=x²: making ƒ surjective by decreasing B=R to B=[0,∞), making ƒ injective by decreasing A=R to A=(−∞,0] (or to A=[0,∞)); inverse function of the function g:(−∞,0]→[0,∞) given by g(x)=x²: g⁻¹(y)=−y^1/2;
  inverse images of sets under a function are well-defined even if the function is not invertible, example: for ƒ:R→R given by ƒ(x)=x², ƒ⁻¹((25,36])=[−6,−5)∪(5,6], ƒ⁻¹({−25})=∅, while ƒ⁻¹(−25) is not well-defined (why?).
  Real numbers: developing the concept of a number: natural numbers N, integers Z, rational numbers Q, real numbers R; axioms of the real numbers - addition and multiplication (click here).
  Reading: Abbott, pages 13, 14.
  FFT problems: Aksoy, problems 1.18, 2.3, 2.5 (on pages 7, 22, 23, solved on pages 15, 27-29)
  Hint on HW 1: the function ƒ:R→R given by ƒ(x)=x² is convenient to construct counterexamples; e.g., think fo examples when the inclusions A⊆ƒ⁻¹(ƒ(A)), B⊆ƒ(ƒ⁻¹(B)) are strict.
• Lecture 4 (Thu, Jan 26): Real numbers (cont.): distributive law; proof that 5+5=2⋅5 from the distributive law and the "definition" of 2 as 1+1; definition of a field - a set with operations addition and multiplication that satisfy the addition axioms, the multiplication axioms, and the distributive law;
  Mini-Theorem 1: uniqueness of 0; Mini-Theorem 2: 0⋅x=0 ∀x (see also Ross, Theorem 3.1(ii)); Mini-Theorem 3: uniqueness of the additive inverse to any x; Mini-Theorem 4: the additive inverse to x is equal to (−1)⋅x (see also Ross, Theorem 3.1(iii));
  group work problems: (1) prove the uniqueness of 1 (hint: see the proof of Mini-Theorem 1), (2) prove the uniqueness of the multiplicative inverse to any x≠0 (hint: see the proof of Mini-Theorem 3).
  Reading: Ross, Theorem 3.1 with proof (pages 15, 16).
  FFT problems: Ross, Sec. 3, Exercises 3.1, 3.2 (page 19); Aksoy, problems 1.18, 2.6 (on pages 7, 23, solved on pages 15, 29).
  The complete Homework 2 is due on February 2 (Thursday).
• Lecture 5 (Tue, Jan 31): Real numbers (cont.): remarks on Additional Problem 2 of Homework 2 on the importance of the order in a mathematical statement, a magic trick based on this;
  order structure (≤); order axioms; ordered fields; properties of ordered fields (Theorem 3.2 of Ross);
  absolute value |a|; distance dist(a,b)=|a−b| between numbers; properties of absolute value (Theorem 3.5 of Ross) - prove part (ii) yourselves, considering all cases (a≥0, b≥0), (a≥0, b≤0), and (a≤0, b≤0); triangle inequality; corollary of the triangle inequality (Corollary 3.6 of Ross).
  The Completeness Axiom: max and min of a nonempty set (Def. 4.1 of Ross); Example - max and min of the sets (a) {-3/2, π, e, 2/5}, (b) [3,7), (c) N, (d) {r∈Q:r²≤2}, (e) {1/n:n∈N}; upper bound and lower bound of a nonempty set, bounded above, bounded below, and bounded sets (Def. 4.2 of Ross); Example (cont.) - upper and lower bounds of the sets (a)-(e); least uppper bound (lub) or supremum (sup) of a nonempty set, greatest lower bound (glb) or infimum (inf) of a nonempty set (Def. 1.3.2 of Abbott); Example (cont.) - sup and inf of the sets (a)-(e); statement of Example 1.3.7 of Abbott.
  Reading: Ross, pages 14-18; Abbott, pages 15-17.
  FFT problems: Aksoy, problems 2.2, 2.9, 2.10 (on pages 22, 23, solutions on pages 27, 31, 32); Abbott, Exercises 1.3.1, 1.3.2 (page 18).
  Just for fun: The curious story of the infamous Indiana Pi bill.
• Lecture 6 (Thu, Feb 2): The Completeness Axiom: Axiom of Completeness (Ross, page 23); example illustrating that the Completeness Axiom does not hold for Q; Example: the supremum of the set c+A, where c∈R, A⊆R, is c+sup(A) (Abbott, Example 1.3.7); Example: (s=sup(A)) ⇔ (∀ε>0 ∃ a∈A s.t. s−ε<a) (Abbott, Lemma 1.3.8 - do the proof yourselves).
  Consequences of Completeness: the Nested Intervals Property (Abbott, Theorem 1.4.1); the Archimedean Property (Abbott, Theorem 1.4.2; do the proof of part (ii) yourselves).
  Reading: Ross, page 23; Abbott, pages 17, 18, 20, 21.
  FFT problems: Aksoy, problem 2.16 (on page 24, solution on pages 34, 35); Abbott, Exercises 1.3.1(b), 1.3.2, 1.3.5, 1.3.8 (on pages 18, 19); Ross, Exercise 4.1 (on page 26).
  Here are the solved exercises on logic and sets that I gave you in class.
  The complete Homework 3 is due on February 9 (Thursday).
• Lecture 7 (Tue, Feb 7): Consequences of Completeness (cont.): group work: finding the suprema of the sets (5,7) and {1/n:n∈N}; density of Q in R (Abbott, Theorem 1.4.3).
  Cardinality: motivation of the need of a rigorous definition of a "number of elements in a set": the set A={1,4,9,16,25,...} of squares of natural numbers is a proper subset of N (i.e., A⊆N and A≠N), but every number n∈N can be put into correspondence with exactly one number n²∈A; 1-to-1 (injective), onto (surjective), and bijective functions (Abbott, Def. 1.5.1); definition of when two sets A and B have the same cardinality (A∼B); the interval (−1,1) has the same cardinality as R as demonstrated by the function ƒ:(−1,1)→R given by ƒ(x)=x/(x²−1) (Example 1.5.4 - figure out all details, i.e., show that ƒ is strictly monotone by computing its derivative, then study the limits of ƒ as x tends to ∞ and −∞, and use the Intermediate Value Theorem from Calculus, or find the explicit expression for the inverse function, ƒ⁻¹:R→(−1,1)); finite, countable, and uncountable sets (Abbott, Def. 1.5.5).
  Reading: Abbott, page 22, Example 1.5.3 on page 26.
  FFT problems: Abbott, Exercises 1.4.1, 1.4.2, 1.4.3, 1.4.4, 1.4.5, 1.4.6, 1.4.8 (on page 24); Aksoy, problems 2.20, 2.27 (on pages 25, 26, solved on pages 36, 37, 39; in problems 2.20 and 2.27, "neighborhood" of x∈R means an open interval centered at x, i.e., an interval of the form (x−ε,x+ε) for some ε>0); if you have time, look at Aksoy, problems 2.14, 2.17 the solution of problem 2.14 is more complicated - read it only if you have time, but do think about its meaning).
• Lecture 8 (Thu, Feb 9): Cardinality (cont.): Q is countable, R is uncountable ([A] Theorem 1.5.6); every set of a countable set is finite or countable ([A], Theorem 1.5.6, without proof); a finite or countable union of countable sets is countable ([A], Theorem 1.5.8, without proof).
  Cantor's Theorem: the interval (0,1) is uncountable ([A], Theorem 1.6.1, proof using Cantor's diagonal argument); power sets - definition and examples; the power set of a finite set A with n elements is 2ⁿ (this explains why sometimes the notation 2^A is used to denote the power set P(A) of a set A) - a heuristic argument by constructing a bijection between the subsets of A and the binary numbers consisting of n digits each of which takes value 0 or 1.
  Reading: Abbott, pages 27-29, 32-34.
  FFT problems: Abbott, Exercises 1.5.2, 1.5.3 (page 30), 1.6.1, 1.6.2, 1.6.3 (pages 32, 33);
  Aksoy, problems 1.11, 2.8 (pages 6, 23).
  The problems Aksoy 1.26 (page 8, solved on page 18) and Abbott 1.5.9 (page 31) are more difficult, but very meaningful - think about them.
  The complete Homework 4 is due on February 16 (Thursday).
• Lecture 9 (Tue, Feb 14): Cantor's Theorem (cont.): Cantor's Theorem (Theorem 1.6.2) on no-existence of a surjective function from a set A to its power set P(A); discussion of equivalence classes of sets by their cardinality (each class consists of sets of the same cardinality)
  The limit of a sequence: sequence - a function with domain N (or {0,1,2,3,...}); convergence of a sequences, limit of a convergent sequence; discussion, elementary examples.
  Reading: Abbott, pages 34-35, 42-46.
  Optional reading: Abbott, Section 1.7, on deeper questions related to cardinality (pages 36-37).
  FFT problems: Abbott, Exercises 1.6.9, 1.6.10(a,b) (page 35), 2.2.2, 2.2.3, 2.2.4 (pages 47, 48);
  Aksoy, problems 3.2, 3.5 (page 42).
• Lecture 10 (Thu, Feb 16): The limit of a sequence (cont.): more examples; uniqueness of limits ([A], Theorem 2.2.7); divergent sequences.
  The algebraic and order limit theorems: bounded sequences; every convergent sequence is bounded ([A], Theorem 2.3.2).
  Reading: Abbott, pages 46, 47, 49.
  FFT problems: Abbott, Exercises 2.2.5, 2.2.7 (page 48); 2.3.2, 2.3.3 (page 54).
• Lecture 11 (Tue, Feb 21): Exam 1 on Sections 1.1-1.6 of Abbott, Section 3 and pages 20-23 of Section 4 of Ross, covered in Lectures 1-8.
• Lecture 12 (Thu, Feb 23): The algebraic and order limit theorems (cont.): Algebraic Limit Theorem ([A], Theorem 2.3.3, prove part (iv) yourselves); Order Limit Theorem ([A], Theorem 2.3.4, prove parts (ii) and (iii) yourselves).
  Reading: Abbott, pages 50-54.
  FFT problems: Abbott, Exercises 2.3.2, 2.3.5, 2.3.6, 2.3.9, 2.3.10(a,c), 2.3.12(b) (pages 54, 55);
  Aksoy, problem 3.15 (page 44).
  The complete Homework 5 is due on March 2 (Thursday).
• Lecture 13 (Tue, Feb 28): The algebraic and order limit theorems (cont.): example: proof that (a_n³+7)/5=8 directly from the definition of convergence and by using the Algebraic Limit Theorem; examples: proving that the sequences (7n²−2)/(11n³), 7n²/(11n³+9), 7n²/(11n³−9), (7n²−2)/(11n³+5n^3/2−9) converge to 0, directly from the definition of convergence.
  The Monotone Convergence Theorem: definition of increasing, decreasing, and monotone sequences; Monotone Convergence Theorem ([A], Theorem 2.4.2); recursively defined sequences; Exercise 2.4.1: proof that the recursively defined sequence x₁=3, x_n+1=1/(4−x_n) converges and computation of its limit.
  Reading: Abbott, pages 56, 57, Exercise 2.4.1.
  FFT problems: Abbott, Exercises 2.4.2, 2.4.3, 2.4.5, 2.4.7 (pages 60, 61);
  Aksoy, problems 3.3, 3.6 (page 42).
• Lecture 14 (Thu, Mar 2): The Monotone Convergence Theorem (cont.): using the Monotone Convergence Theorem to find the resistance of the infinite chain of resistors
  
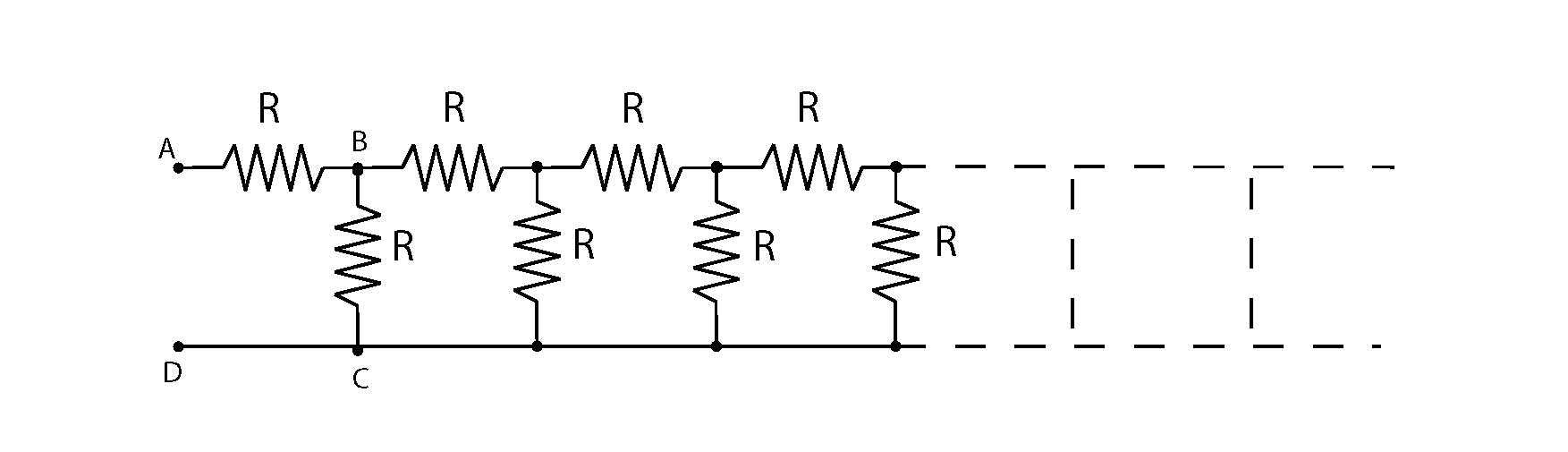
  where R=1Ω, by finding the limit of a recursively defined sequence; expressing the resistance as a continued fraction:
  
  golden mean .
  Subsequences and the Bolzano-Weierstrass Theorem: definition and examples of subsequences; proof all subsequences of a convergent sequence converge to the same limit as the original sequence (Theorem 2.5.2); proof that lim(bⁿ)=0 for b∈(0,1) (Example 2.5.3); proving that a sequence is divergent by finding two subsequences that converge to different limits or, equivalently, by finding a divergent subsequence (Example 2.5.4); Bolzano-Weierstrass Theorem (Theorem 2.5.5) - read the proof from the book, using for inspiration the so-called Bolzano-Weierstrass method for catching a lion in a desert.
  Reading: Abbott, pages 62-64.
  FFT problems: Abbott, Exercises 2.4.4^*, 2.5.4^*, 2.5.7 (the starred problems are mini-theorems and are more difficult);
  Aksoy, problems 2.16 (page 24), 3.23, 3.24, 3.26 (pages 45, 46) - the last three problems will help you understand the concepts of limit superior and limit inferior (which can also be defined in a way different - but equivalent - from the definition in Abbott - see page 41 of Aksoy).
  The complete Homework 6 is due on March 9 (Thursday).
• Lecture 15 (Tue, Mar 7): Subsequences and the Bolzano-Weierstrass Theorem (cont.): Newton's method for computing roots of algebraic equation; the method converges quadratically - a numerical example of computing square root of 2 by using Newton's method;
  proof of Viète's formula
  
  Wallis product
  
  another interesting formula:
  
  The Cauchy criterion: definition of a Cauchy sequence; a_n convergent ⇒ a_n Cauchy (Theorem 2.6.2); a_n Cauchy ⇒ a_n bounded (Theorem 2.6.3); a_n convergent ⇔ a_n Cauchy (Theorem 2.6.4).
  Reading: Abbott, pages 62-64.
  FFT problems: Abbott, Exercises 2.6.2, 2.6.3, 2.6.4(a,b), 2.6.5, 2.6.7(a,b)^* (pages 70, 71) (the starred problems are mini-theorems and are more difficult);
  Aksoy, problems 3.7, 3.10, 3.11, 3.16 (pages 43, 44).
• Lecture 16 (Thu, Mar 9): Open and closed sets: ε-neighborhood V_ε(a) of a point a∈R; open intervals; examples of open set (the empty set, R, an open interval (c,d)); the union of an arbitrary collection of open sets and the intersection of an arbitrary collection of open sets are open (Theorem 3.2.3); limit point (accumulation point, cluster point) of a set; a point x is a limit point of a set iff there exists a sequence (a_n) in A with a_n≠x such that lim(a_n)=x (Theorem 3.2.5); isolated point of a set; closed sets; a subset F⊆R is closed iff every Cauchy sequnce in F converges to an element of F; examples of closed sets; density of Q in R; closure of a set.
  Reading: Abbott, pages 88-91.
  FFT problems: Abbott, Exercise 3.2.1;
  Aksoy, problems 10.1, 10.2, 10.15, 10.16 (pages 198, 200); ∂A means the boundary of the set A (defined in Homework 7); note that Aksoy calls "accumulation point" what we call "limit point", and uses "limit point" with a different meaning (see the definitions on page 197 of that book).
  The complete Homework 7 is due on March 23 (Thursday).
• Lecture 17 (Tue, Mar 21): Open and closed sets (cont.): a convenient characterization of the closure of A: a belongs to the closure of A iff ∀ε>0 V_ε∩A≠∅; the closure of a set A is the smallest closed set containing A (Theorem 3.2.12, without proof); interior of a set - definition (see Exercise 3.2.14), examples; the interior of a set A is the largest open set contained in A; a set is closed iff it is equal to its closure, a set is open iff it is equal to its interior; an set is open iff it complement is closed, an set is closed iff it complement is open (Theorem 3.2.13); the union of a finite collection of closed sets is closed, the intersection of an arbitrary collection of closed sets is closed (Theorem 3.2.14).
  Compact sets: definition of a compact set; definition of a bounded set; a set is compact iff it is closed and bounded (Theorem 3.3.4).
  Reading: Abbott, pages 92, 93, 96, 97.
• Lecture 18 (Thu, Mar 23): Compact sets (cont.): Nested Compact Sets Property (Theorem 3.3.5); open covers, finite subcovers; examples of open covers; Heine-Borel Theorem (Theorem 3.3.8).
  Reading: Abbott, pages 97-99.
  FFT problems: Abbott, Exercises 3.2.7(a), 3.2.8, 3.2.9, 3.2.14 (pages 94, 95); 3.3.1, 3.3.2, 3.3.3, 3.3.4, 3.3.11 (pages 99-101).
  The complete Homework 7a is NOT due on March 28 (Tuesday).
• Lecture 19 (Tue, Mar 28): Functional limits: ε-δ definition of a functional limit; examples; sequential criterion for functional limits (Theorem 4.2.3); algebraic limit theorem for functional limits (Corollary 4.2.4); divergence criterion for functional limits (Corollary 4.2.5); examples.
  Continuous functions: ε-δ definition of continuity; characterizations of continuity (Theorem 4.3.2); criterion for discontinuity (Corollary 4.3.3).
  Reading: Abbott, pages 115-119, 122, 123.
  FFT problems: Abbott, Exercises 4.2.1(a), 4.2.4, 4.2.8, 4.2.10, 4.2.11.
• Lecture 20 (Thu, Mar 30): Exam 2 on Sections 2.2-2.6, 3.2, and 3.3 of Abbott, covered in Lectures 9, 10, 12-18.
• Lecture 21 (Tue, Apr 4): Continuous functions (cont.): algebraic continuity theorem (Theorem 4.3.4); examples; continuity of a composition of continuous functions (Theorem 4.3.9).
  Continuous functions on compact sets: motivation: which properties of sets are preserved when the set is mapped by a continuous function?
  • openness is not preserved - if ƒ:(−1,1)→R is defined as ƒ(x)=x², then ƒ((−1,1))=[0,1),
  • boundedness is not preserved - if ƒ:(0,1]→R is defined as ƒ(x)=1/x, then ƒ((0,1])=[1,∞),
  • closedness is not preserved - if ƒ:R→R is defined as ƒ(x)=1/(1+x²), then ƒ(R)=(0,1]);
  preservation of compact sets (Theorem 4.4.1).
  Reading: Abbott, pages 123-126, 129, 130.
  FFT problems: Abbott, Exercises 4.3.2^*, 4.3.3(b), 4.3.4, 4.3.7 (pages 126, 127).
  The complete Homework 8 is due on April 11 (Tuesday).
• Lecture 22 (Thu, Apr 6): Continuous functions on compact sets (cont.): preservation of compact sets (Theorem 4.4.1); Extreme Value Theorem (Theorem 4.4.2).
  Connected sets: motivation of the concept of a connected set; definition of separated, disconnected, and connected sets; examples of disconnected and connected sets; criterion for connectedness (Theorem 3.4.6, without proof).
  Reading: Abbott, pages 129, 130, 104.
  FFT problems: Abbott, Exercises 3.4.5, 3.4.6 (page 106); 4.4.6(a,c), 4.4.8, 4.4.11, 4.4.12 (pages 134, 135).
• Lecture 23 (Tue, Apr 11): The Intermediate Value Theorem: the Intermediate Value Theorem (IVT) (Theorem 4.5.1); preservation of connected sets (Theorem 4.5.2); proof of the IVT by using the Axiom of Completeness; proof of the IVT by using the Nested Intervals Property; application of the IVT: proof of the existence of a root of an algebraic equation; application of the idea behind the proof of the IVT by using the Nested Intervals Propert: the bisection method for numerical computation of a root of an algebraic equation.
  Derivatives and the Intermediate Value Property: definition of the derivative of a function at a point; differentiable functions; example: computing the derivative of ƒ(x)=xⁿ for n∈N; exercise: prove that ƒ(x)=|x| is not differentiable at 0.
  Reading: Abbott, pages 136-139, 148.
  FFT problems: Abbott, Exercises 4.5.1, 4.5.5 (pages 139, 140).
  The complete Homework 9 is due on April 18 (Tuesday).
• Lecture 24 (Thu, Apr 13): Derivatives and the Intermediate Value Property: a family of functions for constructing (counter)examples: for n∈{0,1,2,...}, define g_n(x)=xⁿsin(1/x) for x≠0 and g_n(x)=0 for x=0:
  • g₀ is discontinuous at 0;
  • g₁ is continuous on R but not differentiable at 0;
  • g₂ is differentiable on R but g₂' is discontinous at 0; ...
  a function differentiable at a point a is continuous at a (Theorem 5.2.3); derivatives of a sum, product, and ratios of two functions (Algebraic Differentiability Theorem, Theorem 5.2.4, do the proof yourself); Chain Rule (Theorem 5.2.5; proof optional); Interior Extremum Theorem (Fermat's Theorem, Theorem 5.2.6); Darboux's Theorem (Theorem 5.2.7).
  Reading: Abbott, pages 146-152 (proof of Theorem 5.2.5 optional).
  FFT problems: Abbott, Exercises 5.2.2, 5.2.3, 5.2.5, 5.2.6, 5.2.9 (pages 152-154).
• Lecture 25 (Tue, Apr 18): The Mean Value Theorems: geometric motivation; Rolle's Theorem (Theorem 5.3.1); Mean Value Theorem (Theorem 5.3.2); g'(x)=0 as a neccessary and sufficient condition for a differentiable function g on an interval to be constant (Corollary 5.3.3); ƒ'(x)=g'(x) implies that ƒ(x)=g(x)+k for some k=const (Corollary 5.3.4); the Generalized Mean Value Theorem (Theorem 5.3.5); L'Hospital's Rule in the case 0/0 (Theorem 5.3.6).
  Reading: Abbott, pages 155-159.
  FFT problems: Abbott, Exercises 5.3.4(a), 5.3.5, 5.3.6 (page 161).
• Lecture 26 (Thu, Apr 20): The Mean Value Theorems (cont.): proof that g'(x)>0 on an interval implies that the g is strictly increasing (proof using the Mean Value Theorem); food for thought: what can we conclude if g'(x)≥0 on an interval?
  A continuous nowhere-differentiable function: a sketch of the ideas in the construction of such a function by using the "sawtooth" function and of the Weierstrass function.
  Rearrangement of infinite series: an explicit rearrangement of the "alternating harmonic series" 1−1/2+1/3−1/4+1/5−1/6+1/7−1/8+... that produces a sum equal to the half of the sum of the original series; if a series is absolutely convergent, then any rearrangement of the series converges to the same limit (Theorem 2.7.10, without proof); Riemann rearrangement ("derangement") theorem: if a series is conditionally convergent (i.e., convergent, but not absolutely convergent), then for any chosen number there exists a rearrangement that converges to that number (with an idea of the proof).
  Uniform convergence of a sequence of functions: definition of pointwise convergence of a sequence of functions (Definition 6.2.1); example: the sequence (ƒ_n) of functions ƒ_n:[0,1]→R defined by ƒ_n(x)=xⁿ converges as n→∞ to the discontinuous function ƒ(x)=0 for x∈[0,1) and ƒ(1)=1 (Example 6.2.2(ii)); definition of uniform convergence of a sequence of functions (Definition 6.2.1); definition of pointwise convergence of a sequence of functions in ε-N terms (Definition 6.2.1B).
  Reading: Abbott, pages 162-165, 39, 40, 75, 173-175, 177.
  FFT: OAThink about the subtle difference between the definition of pointwise convergence and uniform convergence of a sequence (ƒ_n) of functions ƒ_n:A→R to a function ƒ:A→R:
  • (ƒ_n) converges pointwise on A to ƒ if ∀x∈A ∀ε>0 ∃ N s.t. |ƒ_n(x)−ƒ(x)|<ε ∀n≥N;
  • (ƒ_n) converges uniformly on A to ƒ if ∀ε>0 ∃ N s.t. |ƒ_n(x)−ƒ(x)|<ε ∀n≥N and ∀x∈A.
  Notice, in particular, that in the first case N can depend on ε and on x, while in the second case N can depend only on ε (i.e., the same N should work for all x∈A). Use this to prove that the sequence (ƒ_n) of functions ƒ_n:[0,1]→R defined by ƒ_n(x)=xⁿ converges pointwise, but not uniformly, on [0,1].
  The complete Homework 10 is due on April 25 (Tuesday).
• Lecture 27 (Tue, Apr 25) Uniform convergence of a sequence of functions (cont.): a detailed discussion of the concept of uniform convergence of a sequence of functions (contrasted with the pointwise convergence); statement and proof of the continuity of a uniformly continuous sequence of continuous functions (Theorem 6.2.6).
  Reading: Abbott, pages 175-179.
  The complete Homework 10a is NOT due on May 4 (Thursday).
• Lecture 28 (Thu, Apr 27): Exam 3 on Sections 4.2-4.5, 5.2, 5.3, and page 104 of Section 3.4 of Abbott, covered in Lectures 19, 21-25.
• Lecture 29 (Tue, May 2): Uniform convergence and differentiation: idea of the theorem guaranteeing the differentiability of the limit of a sequence of functions (Theorem 6.3.1).
  Series of functions: pointwise and uniform convergence of a series of functions (Definition 6.4.1); term-by-term continuity and term-by-term differentiability of the sum of a series of functions (Theorems 6.4.2 and 6.4.3); Weierstrass M-test (Corollary 6.4.5).
  Power series: derinition of a power series; a power series converges on an interval (open, closed, on open on one side and closed on the other), Theorem 6.5.1, radius of convergence; pointwise convergence of a power series on a set A implies uniform convergence on any compact K⊆A; differentiting a power series (Theorem 6.5.7).
  Reading: Abbott, pages 184; 188, 189; 191; 194, 195.
• Lecture 30 (Thu, May 4): Taylor series: Taylor series of a smooth function (Theorem 6.6.2, with a sketch of proof); "Does the Taylor series of a smooth function converge to the function?" - No: all coefficient in the Taylor series of the function ƒ(x)=0 for x≤0 and ƒ(x)=exp(−1/x²) for x>0 computed from the formula in Theorem 6.6.2 are 0, but the function is not identically 0 in any open interval containing 0; truncating the Taylor series and approximating the function ƒ(x) by a polynomial S_N(x) of degree N, remainder E_N(x)=ƒ(x)−S_N(x), Lagrange's form of the remainder (Theorem 6.6.3); applying the formula for the remainder to give an upper bound on the error in approximating the function ƒ(x) by a Taylor polynomial S_N(x) of degree N; proof of the Lagrange's formula for the remainder (using the generalized Mean Value Theorem).
  Just for fun: explanation of the surprising fact that the Taylor series of the function 1/(1+x²) - which can be obtained by using the formula for the sum of a geometric series, 1/(1+x²)=1/[1−(−x²)]=1−x²+x⁴−x⁶+x⁸−... (as well as the Taylor series of its antiderivative, arctan(x)) - converge only on (−1,1) by observing that 1/(1+x²) has singularities at x=i and x=−i in the complex plane C, so that the circle of convergence of the Taylor series of 1/(1+x²) in C.
  Reading: Abbott, pages 199-202.
• Final Exam: Tuesday, May 9, 8-10 a.m., in 403 PHSC, on the following material:
  • Sections 1.1-1.6 of Abbott, Section 3 and pages 20-23 of Section 4 of Ross, covered in Lectures 1-8;
  • Sections 2.2-2.6, 3.2, and 3.3 of Abbott, covered in Lectures 9, 10, 12-18;
  • Sections 4.2-4.5, 5.2, 5.3, and page 104 of Section 3.4 of Abbott, covered in Lectures 19, 21-25;
  • Section 6.2, covered in Lectures 26, 27 (only the concept of uniform convergence).

Good to know:

• The greek_alphabet.
• Some useful notations.