MATH 5163 - Partial Differential Equations, Section 001 - Spring 2014
TR 12:00-1:15 a.m., 809 PHSC
Instructor:
Nikola Petrov, 802 PHSC, (405)325-4316, npetrov AT math.ou.edu.
Office hours (tentative):
Mon 2:30-3:30 p.m., Thu 1:20-2:30 p.m., or by appointment.
Prerequisites:
Introduction to Partial Differential Equations (MATH 4163) or
permission of instructor.
Course catalog description:
First order equations, Cauchy problem for higher order equations,
second order equations with constant coefficients, linear hyperbolic
equations. (Sp)
Tentative course content:
-
PDEs arising in mechanics, electrodynamics, heat propagation, fluid
dynamics.
-
Laplace's equation, harmonic functions, Dirichlet's Principle, Gauss
Mean Value Theorem and its inverse, Maximum Principle, regularity of harmonic functions,
Liouville's Theorem.
-
Classical Fourier transform (FT) and its inverse, solving PDEs by
using FT. Distributions: definition, convergence, derivatives,
extension of the FT to distributions, properties, examples.
-
Fundamental solutions of Laplace's and Poisson's equations, Green's
functions, method of images, inversion.
-
Heat equation, solution using the FT, uniqueness, fundamental
solutions, non-homogeneous problem, Duhamel's principle.
-
Wave equation. Solution in 1D: D'Alembert's formula, uniqueness by the
energy method. Solution in 3D: fundamental solution, Kirchhoff's
formula, Hadamard's method of descent, Huygens' principle. Fundamental
solutions, non-homogeneous problems.
-
Banach spaces, Hilbert spaces, weak derivatives, Sobolev
spaces. Existence of a weak solution of the Poisson's
equation. Embedding theorems for Sobolev spaces.
-
Eigenfunction expansions, existence and properties of eigenvalues of
certain types of operators, variational principle for the principal
eigenvalue.
-
(If time permits) First-order PDEs: linear, quasilinear (Burgers'
equation), and nonlinear (Hamilton-Jacobi equation).
Text:
The main textbook, freely available online for OU students, will be
S. Salsa.
Partial Differential Equations in Action.
From modelling to theory. Springer, 2008.
We will also use parts of the following books,
freely available online for OU students:
S. Salsa, F. Vegni, A. Zaretti, P. Zunino.
A Primer on PDEs.
Models, methods, simulations.
Springer, 2013 (which significantly overlaps with the main textbook);
A. C. King, J. Billingham, S. R. Otto.
Differential Equations. Linear, nonlinear, ordinary, partial.
Cambridge University Press, 2003.
Homework:
-
Homework 1, due Thu, Jan 23.
-
Homework 2, due Thu, Jan 30.
-
Homework 3, due Thu, Feb 6.
-
Homework 4, due Thu, Feb 13.
-
Homework 5, due Fri, Feb 21, at 4
p.m. in 802 PHSC.
-
Homework 6, due Fri, Feb 28, at 5
p.m. in 802 PHSC.
-
Homework 7, due Fri, Mar 6, at 5
p.m. in 802 PHSC.
-
Homework 8, due Wed, Apr 9, at 5
p.m. in 802 PHSC.
-
Homework 9, due Fri, Apr 18, at 5
p.m. in 802 PHSC.
-
Homework 10, due Fri, May 2, at 5
p.m. in 802 PHSC.
Content of the lectures:
-
Lecture 1 (Tue, Jan 14):
Basic partial differential equations:
classification of partial differential equations (PDEs),
arbitrariness in the general solution of a PDE of order k
for a function of m variables;
a detailed derivation of the heat equation
cρut=∇⋅(k∇u)+Ψ(x,t)
(where Ψ(x,t) is the volume density of the power of
the heat sources inside the domain),
or, for constant k,
ut=α2Δu+ψ(x,t);
derivation of the the boundary conditions for the heat equation:
Dirichlet condition (the temperature is controlled at the boundary),
Neumann condition (the heat flux is controlled at the boundary),
Robin condition (convective heat exchange with the surroundings)
[Sec. 1.2]
-
Lecture 2 (Thu, Jan 16):
Other important partial differential equations:
diffusion equation, wave equation, Poisson and Laplace equations,
Schrodinger equation, Maxwell's equations, Navier-Stokes equations.
Domains and Green's identities:
Ck-domains;
Divergence Theorem, Green's identities.
Properties of harmonic functions:
definition of harmonic functions;
uniqueness of the solution of Poisson equation with Dirichlet boundary
conditions;
energy of a vibrating membrane, energy of a membrane
in equilibrium in the Earth's gravity field.
-
Lecture 3 (Tue, Jan 21):
Properties of harmonic functions (cont.):
Dirichlet's principle: harmonic functions minimize the energy
functional, and the minimizer of the energy functional is a harmonic
function;
average values over a ball and a sphere: definitions;
Mean Value Theorem for harmonic functions;
Maximum Principles: statement of the weak and the strong maximum
principles (the proof will be given in Lecture 4);
if "max" is replaced by "min", then we obtain a "minimum principle"
(because if u is harmonic, then −u
is also harmonic, and the maxima of u are minima of
−u and vice versa);
physical interpretation: the maximum or minimum of a steady-state
temperature distribution in absence of source in the domain
cannot occur inside the domain, but only on the boundary.
-
Lecture 4 (Thu, Jan 23):
Properties of harmonic functions (cont.):
Maximum Principles: proof of the strong maximum principle;
uniqueness of the solution of the Poisson equation
(proof by using the Maximum Principle);
explicit solutions of the Poisson equation in a ball
in 2 and 3 dimensions, regularity of these solutions,
regularity of harmonic functions in an arbitrary domain;
derivative estimate for harmonic functions;
Liouvile Theorem.
-
Lecture 5 (Tue, Jan 28):
Fourier transform − an introduction:
Lp spaces;
integral transform, integral kernel;
Fourier transform (FT) − definition,
proof that it maps
L2(R) to L∞(R),
examples, elementary properties;
convolution, the Convolution Theorem;
Inverse FT, the Inversion Theorem,
an example of using the Inversion Theorem;
Dirac δ-function δa − a heuristic definition,
FT of δa, using the Inversion Theorem
to obtain an integral representation of δ;
Parseval's Theorem (Plancherel's Theorem)
− proof of the theorem and remarks on its physical meaning.
Using FT to solve PDEs:
using FT to solve the heat equation on R.
-
Lecture 6 (Thu, Jan 30):
Using FT to solve PDEs (cont.):
using FT to solve Laplace's equation (i.e., the steady-state heat
equation) in the half-plane x∈R, y>0.
Test functions and mollifiers:
support of a function, examples, compactly supported functions,
the "standard" compactly supported function η supported on the
closed unit ball in Rn,
and its rescaled version ηε
supported on the closure of B(0,ε);
Young's Theorem;
mollifiers, using a mollifier to regularize a "rough" function ƒ
by convolving them with ηε;
properties of the convolution
ƒ∗ηε (Lemma 7.1);
locally integrable functions
[pages 369-372 of Sec. 7.2]
-
Lecture 7 (Tue, Feb 4):
Test functions and mollifiers (cont.):
discussion of some properties of the convolution
ƒ∗ηε
(Remarks 7.1 and 7.2, Example 7.2),
density of the space of smooth compactly supported functions
on Ω in Lp(Ω)
for any p∈[1,∞)
(Theorem 7.1, without proof)
[pages 178, 179 of Sec. 3.2]
Distributions:
multiindex notations in Rn:
α=(α1,...,αn)
where αj∈{0,1,2,...},
length |α| of the multiindex defined as the sum of
its components αj,
differential operator
Dα=∂|α|/∂x1α1...∂xnαn,
product of components
xα=(x1)α1...(xn)αn;
the space D(Ω) of test functions as the set of compactly
supported smooth functions with an appropriately defined meaning of
convergence; examples;
the set D'(Ω) of distributions as continuous linear
functionals on D(Ω),
examples of distributions coming from L2 functions or from locally integrable
functions; linear combinations of distributions;
continuous embeddings of Lp(Ω)
into the space of locally integrable functions on Ω
and of the space of locally integrable functions on
Ω into the space of distributions D'(Ω),
proof of the continuity of the second embedding
[pages 373-375 of Sec. 7.3]
-
Lecture 8 (Thu, Feb 7):
Distributions (cont.):
Holder inequality;
example: the locally integrable function 1(x)≡1 defines a
distribution;
example: Dirac comb
[pages 375-376 of Sec. 7.3]
Calculus:
motivation of the definition of a derivative of a distribution,
definition of a derivative of a distribution
F∈D'(Ω) for
Ω⊆Rn:
⟨DαF,φ⟩:=(−1)|α|⟨F,Dαφ⟩,
where
φ∈D(Ω) is an arbitrary test
function;
examples;
proof that the derivative of the Heaviside function H is
the Dirac function δ
(and Ha'=δa)
[pages 377-379 of Sec. 7.4]
-
Lecture 9 (Tue, Feb 11):
Calculus (cont.):
continuity of differentiation in D'(Ω) (Proposition 7.3);
vector-valued test functions
φ∈D(Ω,Rn)
and
vector valued distributions
F∈D'(Ω,Rn);
pairing between elements
of D'(Ω,Rn)
and elements of
D(Ω,Rn);
gradient of
ƒ∈D'(Ω)
(with Ω⊆Rn),
⟨∇ƒ,φ⟩=−⟨ƒ,∇⋅φ⟩;
divergence of
F∈D'(Ω,Rn),
⟨∇⋅F,φ⟩=−⟨F,∇φ⟩;
Laplacian of
ƒ∈D'(Ω),
⟨Δƒ,φ⟩=⟨ƒ,Δφ⟩;
derivation of the fundamental solution of the Laplacian operator
in R3:
−Δu=δ
[pages 379-382 of Sec. 7.4]
Multiplication, composition, division, convolution:
impossibility of defining multiplication of distirbutions;
multiplying a distribution by a C∞ function
[pages 382-383 of Sec. 7.5]
-
Lecture 10 (Thu, Feb 13):
Multiplication, composition, division, convolution (cont.):
more multiindex notations:
α!=α1!...αn!,
β≤α if
βj≤αj for all
j=1,...,n,
α−β=(α1−β1,...,αn−βn)
defined for β≤α,
α "choose" β is defined as
α!/[β!(α−β)!];
Leibniz rule for the derivative of a product of a smooth function
and a distribution, examples;
problems with defining a composition of a distribution with a
smooth function, defining a composition of a distribution and a 1-to-1
smooth function with a smooth inverse, example: delta function of a
function of x with simple zeros;
dividung a distribution by a smooth function that never vanishes,
dividing a distribution by a smooth function with zeros
(possibly of higher multiplicities) (Proposition 7.4),
principal value of an integral, distribution
P.v.(1/x)∈D'(R),
the general solution of the equation xG=1
is G=P.v.(1/x)+Cδ
(where C is an arbitrary constant);
problems with defining the convolution of two distributions,
support of a distribution, distributions with compact support,
definition of the convolution of a distribution with compact support
and a smooth function,
the convolution of a distribution with compact support and a
C∞ function is a
C∞ function (Proposition 7.5),
the delta function is the identity with respect to convolution
[pages 383-388 of Sec. 7.5]
-
Lecture 11 (Tue, Feb 18):
Tempered distributions:
need for using another space of test functions in order to define
Fourier transform (FT) for the corresponding distributions
(footnote on page 388);
space S(Rn) of
functions rapidly vanishing at ∞ (rapidly decreasing), examples;
definition onf convergence of a sequence
in S(Rn);
D(Rn)⊂S(Rn);
if
(vk)⊂D(Rn)
converges to
v in D(Rn),
then
(vk)⊂S(Rn)
and vk→v
in S(Rn);
space S'(Rn) of tempered distributions
(giving the definition in stages);
D(Rn)⊂S(Rn)⊂Lp(Rn)⊂S'(Rn)⊂D'(Rn);
completeness of S'(Rn);
definition of convergence of a sequence of tempered distributions;
example: the Dirac comb as an element
of S'(Rn);
the convolution of a tempered distribution and a rapidly decreasing
function is a tempered distribution which coincides with a
C∞ function
[Sec. 7.6.1]
FT in S'(Rn):
direct and inverse FTs
on Lp(Rn) functions;
continuity of the direct and the inverse FT;
weak Parseval identity;
definition of a FT of a tempered distribution;
properties of the FT on S'(Rn)
(please read them from the book);
examples: FT of 1, FT of the coordinate
function xj
[Sec. 7.6.2]
-
Lecture 12 (Thu, Feb 20):
FT on L2(Rn):
u∈L2(Rn)
if and only if its FT is
in L2(Rn);
strong Parseval identity (i.e., the FT is an isometry in
L2(Rn),
up to a factor); an example of application of the strong Parseval
identity
[Sec. 7.6.3]
Laplace and Poisson equations:
fundamental solution of a linear differential operator;
derivation of the fundamental solution Φ(x)
of the Poisson's equation in R3 by using FT
[recall that we verified by a direct integration
that Φ(x)=1/(4π|x|) is
a fundamental solution of Poisson's equation
in R3 in Lecture 9];
applying a Green formula to the case when one of the functions
is Φ(x)=1/(4π|x|)
[Sec. 3.5.1]
-
Lecture 13 (Tue, Feb 25):
Laplace and Poisson equations (cont.):
definition of the Green function of the operator −Δ
in a domain Ω⊂Rn,
general properties: positivity, symmetry;
derivation of the Green function of −Δ
in the upper half-space
{x∈R3:x3>0}
- the method of electrostatic images;
derivation of the Green function of −Δ
in a ball
BR(0)⊂R3
- an image charge located at the inversion of
x∈BR(0);
Green representation formula for the solution of the Dirichlet BVP
−Δu(x)=ƒ(x) for
x∈Ω⊂Rn,
u(x)=g(x) for
x∈∂Ω,
single and double layer potentials, Poisson kernel;
solution of the Dirichlet BVP in the upper half-space
of R3
[pages 133-136 of Sec. 3.5.2 and 3.5.3]
-
Lecture 14 (Thu, Feb 27):
Laplace and Poisson equations (cont.):
Poisson kernel and Poisson formula for the solution of the Dirichlet
BVP for the Poisson equation in a ball of radius R
in R3;
the Neumann BVP for the Poisson equation in bounded domain
- compatibility condition between the equation and the boundary
condition, and how to take care of this condition
in finding Neumann function (i.e., the Green function in this case)
[pages 137, 138 of Sec. 3.5.3 and 3.5.4]
-
Lecture 15 (Tue, Mar 4):
The heat/diffusion equation:
discussion of the physical meaning of the heat and diffusion equations
and the Dirichlet, Neumann, and Robin boundary conditions;
the linearity of the homogeneous equation
ut−α2Δu=0
implies the Principle of Superposition of solutions
[pages 13-18 of Sec. 2.1]
Uniqueness:
integral method of proving the uniqueness of the solution
of the heat equation for the three boundary conditions
[pages 30, 31 of Sec. 2.2]
The fundamental solution:
time reversal in the heat equation;
invariance of the heat equation with respect of space and time
translations;
parabolic dilations - constructing a dimensionless expression
x/(αt1/2) that does not change
under the transformations
x→ax,
t→a2t
with respect to which the homogeneous heat equation is invariant
[pages 34-35 of Sec. 2.3]
-
Lecture 16 (Thu, Mar 6):
The fundamental solution (cont.):
dilation and conservation of mass - if we perform a dilation
x→ax, t→a2t,
u→cu, then conservation of mass
(for the diffusion equation) implies that
c=an (where n is the
dimension of the space Rn);
looking for the fundamental solution of the heat equation
in R×(0,∞) in the form
Γ(x,t)=A/(αt1/2)v(ζ),
where A is a dimensionless constant,
ζ=x/(αt1/2),
and v is an unknown function of one variable
- this substitution leads to an ODE for v(ζ)
which together with some appropriate conditions leads
to the fundamental solution
Γ(x,t)=1/(2α(πt)1/2)exp{−x2/(4α2t)}
in R×(0,∞)
(this calculation was done in Problem 1 of Homework 5);
obtaining the fundamental solution of the heat equation
in R×(0,∞) by Fourier transform
with respect to the spatial variable x (done in Lecture 5);
generalization - looking for the fundamental solution of the heat equation
in Rn×(0,∞) in the form
Γ(x,t)=A/(αt1/2)v(ζ),
where A is a dimensionless constant,
ζ=|x|/(αt1/2),
and v is an unknown function of one variable
- this substitution leads to an ODE for v(ζ)
which yields the fundamental solution
Γ(x,t)=1/(4α2πt)n/2exp{−|x|2/(4α2t)}
in Rn×(0,∞)
[pages 35-38, 42, 43 of Sec. 2.3]
-
Lecture 17 (Tue, Mar 11):
Exam 1
-
Lecture 18 (Thu, Mar 13):
The global Cauchy problem:
recall that the fundamental solution on
(x,t)∈Rn×(0,∞),
=\frac{1}{2\alpha\sqrt{\pi t}}
\exp\left(-\frac{|\mathbf{x}|^2}{4\alpha^2 t}\right) ,
)
satisfies the initial-value problem
on (x,t)∈Rn×(0,∞)
 \, \Gamma(\mathbf{x},t)=0 , \quad
\quad \Gamma(\mathbf{x},0)=\delta(\mathbf{x}) ,
)
and notice that it also satisfies
on (x,t)∈Rn×(0,∞)
 \, \Gamma(\mathbf{x},t)
=\delta(\mathbf{x}) \delta(t) , \quad
\quad \Gamma(\mathbf{x},0)=0;
)
because of translational invariance, for given
y∈Rn
and s∈(0,∞),
the solution
on (x,t)∈Rn×(s,∞)
of the initial value problem
 \, u(\mathbf{x},t)
= 0 , \quad
\quad u(\mathbf{x},s)=\delta(\mathbf{x}-\mathbf{y})
)
or, equivalently,
 \, u(\mathbf{x},t)
=\delta(\mathbf{x}-\mathbf{y}) \delta(t-s) , \quad
\quad u(\mathbf{x},s)=0
)
is

=\frac{1}{2\alpha\sqrt{\pi (t-s)}}
\exp\left(-\frac{|\mathbf{x}-\mathbf{y}|^2}{4\alpha^2 (t-s)}\right) ;
)
by the Principle of Superposition,
the solution of the initial-value problem
on
(x,t)∈Rn×(0,∞)
 \, u(\mathbf{x},t)
=f(\mathbf{x},t) , \quad
\quad u(\mathbf{x},0)=g(\mathbf{x})
)
is ("Duhamel's principle")
 =
\int_0^t \int_{\mathbf{R}^n}\Gamma(\mathbf{x}-\mathbf{y},t-s)
\, f(\mathbf{y},s) \, \mathrm{d}\mathbf{y} \, \mathrm{d}s
+ \int_{\mathbf{R}^n}\Gamma(\mathbf{x}-\mathbf{y},t)
\, g(\mathbf{y}) \, \mathrm{d}\mathbf{y} ;
)
using physics arguments to solve PDEs:
advection-diffusion-reaction equation describing
the evolution of the concentration
u(x,t) of a pollutant in a channel
in which the water is moving in positive direction
with velocity c and the pollutant is decaying
exponentially in time:
 = g(x) :
)
if y=x−ct
is the coordinate in the coordinate system
"comoving" with the water,
and u(x,t)=v(x−ct,t),
where v(y,t) is the concentration of the
pollutant in the comoving coordinate system,
then v(y,t) satisfies
 = g(y) ;
)
since if v(y,t) satisfies does not depend
on y, then u will decay exponentially with time,
we set
v(y,t)=e−γtw(y,t),
and the new unknown function w(y,t) satisfies
the diffusion/heat equation
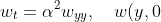 = g(y) ,
)
so by Duhamel's principle
 =
\mathrm{e}^{-\gamma t} \, w(y,t)|_{y=x-ct} =
\mathrm{e}^{-\gamma t}
\int_{\mathbf{R}}\Gamma(x-ct-z,t)\,g(z)\,\mathrm{d}z
)
[pages 68, 69, 71-73 of Sec. 2.8;
pages 54-57 of Sec. 2.5, Problem 1 of Homework 3]
-
Lecture 19 (Tue, Mar 25):
Waves and vibrations - general concepts:
important particular cases: travelling waves,
harmonic waves; plane waves, spherical waves;
important concepts: amplitude, wave number, wavelength,
angular frequency, period, linear frequency,
phase speed, (group speed)
[pages 221-223 of Sec. 5.1]
Transversal waves in a string:
the equation describing transversal waves in a string
(without derivation);
energy in the waves in a string, conservation of energy
[pages 226, 228, 229 of Sec. 5.2]
The one-dimensional wave equation:
equation, initial conditions, and different boundary conditions
(Dirichlet, Neumann, Robin) for one-dimensional waves;
principle of superposition for the homogeneous wave equation
[pages 229-231 of Sec. 5.3]
The d'Alembert formula:
changing the variables (x,t) to
η=x−ct and
ζ=x+ct;
general solution of the 1-D wave equation on R:
u(x,t)=φ(x−ct)+ψ(x+ct);
relating the functions φ and ψ with the initial conditions
- d'Alembert formula;
range of influence, domain of dependence, speed of propagation of the signal
[pages 236-238 of Sec. 5.4]
-
Lecture 20 (Thu, Mar 27):
The d'Alembert formula (cont.):
remark about factorizing the wave operator:
∂tt−c2∂xx=(∂t+c∂x)(∂t−c∂x),
uni- and bidirectional wave equations (unidirectional of first order,
bidirectional of second order in time);
demonstrating the well-posedness of the 1-D wave equation on a finite
time interval from the d'Alembert formula for the solution;
the fundamental solution K(x,y,t)
of the 1-D wave equation - a derivation from the d'Alembert formula;
derivation of the d'Alembert formula by using the expression
for K(x,y,t);
non-homogeneous equation - Duhamel's method, physical interpretation
[pages 238, 244-247 of Sec. 5.4]
-
Lecture 21 (Tue, Apr 1):
The d'Alembert formula (cont.):
formal derivation of the expression for the solution of the
nonhomogeneous 1-D wave equation with nonzero initial conditions
by using the fundamental
solution K(x,y,t).
The Cauchy problem:
fundamental solution K(x,t)
of the 3-D wave equation - derivation by using
Fourier transform in the spatial variable,
delta-function concentrated on a sphere and its Fourier transform;
using the fundamental solution to derive solution
for zero initial displacement u(x,0)
and non-zero initial velocity ut(x,0);
using the fundamental solution to derive solution
for non-zero initial displacement u(x,0)
and zero initial velocity ut(x,0);
Kirchhoff formula; Huygens principle
[pages 274, 275, 277-279 of Sec. 5.9]
-
Lecture 22 (Thu, Apr 3):
The Cauchy problem (cont.):
nonhomogeneous problem, Duhamel's principle,
retardation effects due to the finite speed
of propagation of the waves;
Hadamard's method of descent for deriving the solution
of the wave equation in two spatial dimensions
by using the solution in three spatial dimension
given by Kirchhoff's formula,
fundamental solution of the wave equation in two spatial dimensions,
Huygens principle does not hold in two spatial dimensions;
physical interpretation of Hadamard's method of descent
- the fundamental solution of the wave equation in two spatial
dimensions can be obtained as the solution of the 3-dimensional
wave equation with a source term spread along the x3-axis,
i.e., equal to
δ(x1)δ(x2)δ(t)
- therefore, one can obtain the fundamental solution
K(2)(x1,x2,t)
by integrating the fundamental solution
K(3)(x1,x2,x3,t)
with respect to x3 (from −∞ to ∞)
[pages 279-282 of Sec. 5.9]
-
Lecture 23 (Tue, Apr 8):
Norms and Banach spaces:
norm, normed linear space; distance, metric space;
convergent sequence in a metric (or normed) space,
Cauchy sequence; convergent implies Cauchy;
complete normed space, Banach space;
continuous operator; continuity of the norm;
space C(A) of continuous functions
(for A⊂Rn compact),
sup (max) norm on C(A),
completeness of C(A) with the sup norm
(i.e., C(A) with the sup norm is a Banach space);
L2(A) norm on C(A),
this normed space is not complete;
Ck(A) wiht the maximum norm
of order k is a Banach space;
sets of measure zero, functions equal almost everywhere (a.e.)
in an open set Ω, equivalence classes of functions
that differen only on subsets of measure zero,
essentially bounded functions, essential supremum,
spaces Lp(A)
for p∈[1,∞)
and L∞(A);
Holder inequality
[pages 307-311 of Sec. 6.2]
Hilbert spaces:
inner product, inner product linear space;
norm induced by an inner product; Schwarz inequlity;
Hilbert space; isomorphism between two Hilbert spaces;
example: Rn with the Euclidean inner product
or with a more general inner product defined by a symmetric
positive-definite matrix;
example: L2(Ω)
[pages 311-314 of Sec. 6.3]
-
Lecture 24 (Thu Apr 10):
Hilbert spaces (cont.):
example: space l2 of sequences;
elementary facts about Fourier series;
example: a Sobolev space of periodic functions
[pages 314, 315 of Sec. 6.3; pages 531-533 of Appendix A]
Projections and bases:
basis of a linear space; dimension of a linear space;
orthogonality of vectors in an inner product linear space;
orthogonal and orthonormal bases in an inner product linear space;
finding the components of a vector in an orthogonal or an orthonormal
basis; projections in Rn;
orthogonal direct
sum Rn=V⊕V⊥
[pages 316-318 of Sec. 6.4]
Sobolev spaces:
definitions of Cr0(Ω)
(i.e., Cr functions whose support
is a compact set contained completely in the interior of Ω),
test functions D(Ω), distributions D'(Ω),
L1loc(Ω)
for Ω⊂Rn;
weak derivatives - derivatives in the sense of distribution
that are in L1loc(Ω).
-
Lecture 25 (Tue, Apr 15):
A digression on the wave equation:
waves in a guitar string,
flageolets - supressing some harmonics by touching the string at
certain positions, see the Wikipedia article
Harmonic.
Sobolev spaces (cont.):
examples of weak derivatives;
Sobolev spaces
Wk,p(Ω), norm in
Wk,p(Ω),
Wk,p(Ω) is a separable
Banach space;
Sobolev spaces
Hk(Ω)=Wk,2(Ω),
Hk(Ω) is a Hilbert space,
inner product and norm in Hk(Ω);
the space H1(Ω);
functions from H1(Ω)
have finite energy;
digression: separability, sketch of the proof of the separability of
the space C(Ω) for compact
Ω⊂Rn based on Weierstrass
Approximation Theorem, every Hilbert space admints an orthonormal
basis, separability of the spaces Lp(Ω)
for p∈[1,∞);
Theorem: H1(Ω) is a separable Hilbert space,
continuously embedded in L2(Ω),
and the gradient operator is continuous
from H1(Ω) to L2(Ω)
[pages 320, 321 of Sec. 6.4; pages 396, 397 of Sec. 7.7]
-
Lecture 26 (Thu, Apr 17):
Sobolev spaces (cont.):
the
function u(x)=(−log(|x|))a
belongs to
H1(Ω) for
Ω={x∈|R2:0<|x|<1}
and a<1/2;
characterization of H1([a,b]);
definition of H10(Ω)
as the closure of D(Ω) in H1(Ω);
Poincare inequality in H10(Ω)
for bounded domain Ω; inner product
(u,v)1:=(∇u,∇v)0
and norm
||u||1:=(u,v)11/2
in H10(Ω)
(equivalent to the norm
||u||1,2:=(u,v)1,21/2
in H1(Ω))
[pages 397-400 of Sec. 7.7]
-
Lecture 27 (Tue, Apr 22):
Sobolev spaces (cont.):
the dual H−1(Ω)
of H10(Ω);
the elements of H−1(Ω)
are distributions from D'(Ω);
characterization of H−1(Ω)
as the distributoins of the form
F=g+div(h)
for g∈L2(Ω)
and h∈L2(Ω,Rn);
δ0∈H−1((−a,a))
but
δ0∉H−1(Ω)
where Ω is a subset of Rn
for n≥2; example: ∇χΩ;
definition of the spaces
Hm(Ω) for m>1
[pages 401-403 of Sec. 7.7]
Classical, strong, and weak solutions of Poisson equations with
homogeneous Dirichlet BCs:
Classical solution: given
ƒ∈C(cl(Ω)),
find
u∈C2(Ω)∩C(cl(Ω))
such that −Δu(x)=ƒ(x)
classically in Ω and u(x)=0
for x∈∂Ω;
strong solution: given
ƒ∈L2(Ω),
find
u∈H2(Ω)∩H10(Ω)
such that −Δu=ƒ with derivatives understood
in weak sense.
-
Lecture 28 (Thu, Apr 24):
Classical, strong, and weak solutions of Poisson equations with
homogeneous Dirichlet BCs:
using Green's formula to derive the weak formulation
of the Poisson problem:
given
ƒ∈H−1(Ω),
find
u∈H10(Ω)
such that (u,v)1=⟨ƒ,v⟩
for any v∈H−1(Ω),
where ⟨ƒ,v⟩ is the dual pairing
and the derivatives are understood in weak sense;
using Riesz representation theorem
to prove existence and uniqueness of the weak solution
of Poisson's equation;
a generalization: weak formulation of the Poisson's problem
−∇⋅[a(x)∇u(x)]=ƒ(x)
classically in Ω and u(x)=0
for x∈∂Ω,
where 0<μ≤a(x)≤ν;
proof of existence and uniqueness by defining an inner product
equivalent to the standard inner product in
H10(Ω).
-
Lecture 29 (Tue, Apr 29):
Classical, strong, and weak solutions of Poisson equations with
homogeneous Dirichlet BCs (cont.):
another generalization: anisotropic heat conductivity
- the heat flux density j has components
ji(x,t)=aik(x) ∂u(x,t)/∂xk;
abstract variational problems.
Abstract variational problems:
bilinear forms (sesquilinear in the complex case), examples;
abstract variational problem:
for a bilinear form a on a Hilbert V
and a linear functional F∈V*,
find u∈V such that
a(u,v)=⟨F,v⟩*
for all v∈V; Lax-Milgram Theorem (Theorem 6.5),
stability estimate
[pages 334-336 of Sec. 6.6]
-
Lecture 30 (Thu, May 1):
Abstract variational problems (cont.):
for a symmetric bilinear form, the abstract variational problem
is equivalent to the problem of minimizing the quadratic
functional
E(v)=(1/2)a(v,v)-⟨F,v⟩*
(Theorem 6.7); first variation of a linear functional, Euler equation;
filtration of nested supspace of a linear space:
…⊂Vk⊂Vk+1⊂…
projections;
projected prolem, stiffness matrix, Galerkin method
[pages 339-342 of Sec. 6.6]
-
Final exam:
Friday, May 9, 1:30-3:30 p.m.
Grading:
Your grade will be determined by your performance
on the following coursework:
| Coursework |
Weight |
| Homework (lowest grade
dropped) |
30% |
| Two midterm exams (20%
each) |
40% |
| Final Exam |
30% |
Homework:
It is absolutely essential to solve the assigned homework problems!
Homework assignments will be given regularly throughout the semester
and will be posted on this web-site. The homework will be due at the start
of class on the due date. Each homework will consist of several problems,
of which some pseudo-randomly chosen problems will be graded. Your lowest
homework grade will be dropped.
Your homework should have your name clearly written on it,
and should be stapled.
No late homeworks will be accepted!
Exams:
There will be two in-class midterms and a comprehensive in-class final exam.
Tentative dates for the midterms are
February 25 (Tuesday) and April 17 (Thursday).
The final exam is scheduled for May 9 (Friday), 1:30-3:30 p.m.
All tests must be taken at the scheduled times,
except in extraordinary circumstances.
Please do not arrange travel plans that prevent you
from taking any of the exams at the scheduled time.
Attendance:
You are required to attend class on those days when an
examination is being given; attendance during other class periods is also
strongly encouraged.
You are fully responsible for the
material covered in each class, whether or not you attend.
Make-ups for missed exams will be given only if
there is a compelling reason for the absence,
which I know about beforehand
and can document independently of your testimony
(for example, via a note or a phone call from a
doctor or a parent).
Useful links:
the
academic
calendar.
Policy on W/I grades :
From January 13 to January 27, you can withdraw
from the course without record of grade.
From January 28 to February 21, graduate students can withdraw
from the course with an automatic "W" (for undergraduate students
this period is January 28 to March 28).
After this you may petition to the Dean
to withdraw and receive a "W" or "F" grade
according to your standing in the class.
(Such petitions are not often granted.
Furthermore, even if the petition
is granted, I will give you a grade
of "Withdrawn Failing" if you are
indeed failing at the time of your petition.)
Please check the dates in the Academic Calendar!
The grade of "I" (Incomplete)
is not intended to serve as
a benign substitute for the grade of "F".
I only give the "I" grade
if a student has completed the majority
of the work in the course
(for example everything except the final exam),
the coursework cannot be completed
because of compelling and verifiable problems
beyond the student's control, and the student expresses a clear
intention of making up the missed work as soon as possible.
Academic misconduct: All cases of suspected academic misconduct will
be referred to the Dean of the College of Arts and Sciences for prosecution
under the University's Academic Misconduct Code. The penalties can be quite
severe. Don't do it!
For details on the University's
policies concerning academic integrity see the
Student's Guide to Academic Integrity
at the
Academic Integrity web-site.
For information on your rights to appeal charges
of academic misconduct consult the
Academic Integrity Code.
Please check out the web-site of the
OU Student
Conduct Office.
Students with disabilities:
The University of Oklahoma is committed to providing reasonable accommodation
for all students with disabilities. Students with disabilities who require
accommodations in this course are requested to speak with the instructor
as early in the semester as possible. Students with disabilities must be
registered with the Office of Disability Services prior to receiving
accommodations in this course. The Office of Disability Services is located
in Goddard Health Center, Suite 166: phone 405-325-3852 or TDD only
405-325-4173.
Good to know: